De filterschakelingen.
|
Filters zijn samengesteld uit elementen die we al in de beginnen van deze cursus gezien hebben. Deze basiselementen zoals condensatoren, spoelen ... laten toe om wat meer complexe samenstellen met specifieke eigenschappen te verwezenlijken. |
||||||||||||||
|
De noodzaak van filtrers : |
||||||||||||||
|
Een radio of zender bevat heel wat filters daar zij onontbeerlijk zijn voor de goede werking. Bij een ontvanger, als voorbeeld, is het frequentie spectrum van ontvangst zeer uitgebreid. We moeten enkel een klein deeltje met een keer bewerken (of beluisteren). |
Het is als het ware een venster dat we over het volledige frequentiespectrum gaan plaatsen. Al wat buiten het venster ligt interesseert ons niet. Door dat venster zijn we selectief wat de ontvangst betreft. |
|||||||||||||
|
Van het laagfrequent signaal dat we gaan gebruiken om bv gehoord te worden of als data voor digitale communicatie moet liefst niet uitgebreider zijn dan nodig maar toch juist voldoende. Wie zei het weer "trop c'est trop". Ongewenste harmonische gaan we elimineren. |
Al dat werk zullen gespecialiseerde kringen voor ons klaren. Deze kringen heten : |
|||||||||||||
|
De rol van het filter is dus het verwijderen of ten minste verminderen van een deel van het oorspronkelijk spectrum van het signaal bij de ontvangst. Goed gedimensioneerde basis elementen, oordeelkundig samen gevoegd tot filters zullen bij minimaal verzwakken het nuttig signaal doorlaten of blokkeren al naar gelang het geval. |
||||||||||||||
|
Soorten filters : |
||||||||||||||
|
Naar gelang het gebruik kunnen we het filter in 4 soorten onderverdelen: |
||||||||||||||
|
||||||||||||||
|
De vier hoger getoonde doorlaatcurven, de winst (verzwakking is negatieve winst ! ) staat in functie van de frequentie. De vertikale as toont ons de winst en de horizontale de frequentie van het aan gelegde signaal . |
||||||||||||||
|
En hoe werkt het nu ? |
||||||||||||||
|
Gezien het filter is samengesteld uit passieve elementen , condensator/spoel, en hun gedrag op wisselspanning tegengesteld en functie van de frequentie, gaan we door van deze eigenschappen gebruik te maken een of andere gedrag bepalen. Let er op, het is de reactantie bij deze componenten waar het over gaat. |
||||||||||||||
|
Bij gebruik van condensator zal bij stijgende frequentie de impedantie Z dalen. |
Bij gebruik van spoel gebeurt het omgekeerde. |
|||||||||||||
|
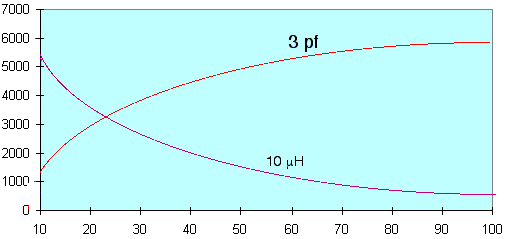
We besluiten dat een condensator zich als laagdoorlaat gedraagt. De REACTANTIE is dalend bij stijgende frequentie. |
Een spoel gedraagt zich als een hoogdoorlaat bij stijgende frequentie. De REACTANTIE vergroot met de frequentie. |
|||||||||||||
 |
||||||||||||||
|
Wat U hierboven ziet zijn curven van een 10 µH spoel en een condensator van 3 pF voor een frequentie gaande van 10 tot 100 MHz. |
||||||||||||||
 +
+  |
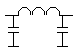
Bekijken we nu de links getekende filters in functie van hun gedrag ten opzichte de frequentie. Bij lage (relatief) frequentie is de reactantie van de spoel zwak, maar deze van de condensator daartegenover groot. Aangesloten op een laagfrequent signaal zien we de impedantie als zeer groot . De spoel biedt maar weinig weerwerk en mag klein gezien worden. Aan de uitgang van het filter verschijnt bijna het volledige ingangssignaal. |
|||||||||||||
|
Laten we nu de frequentie stijgen. De reactantie van de spoel vergroot en deze van de condensatoren daar en tegen verkleinen. Het gevolg hiervan is dat op de ingang een kleiner impedantie verschijnt. Maar doorheen het filter zien we een groter wordende impedantie. Bij nog stijgende frequentie vergroot dit effect. Aan de uitgang zien we een steeds kleiner wordend deel van de ingang. De bron wordt belast met een kleine reactantie (kleiner deel van het signaal) en daarop volgt een spanningsdeler welke het uitgangssignaal nog maar zal verkleinen. |
||||||||||||||
|
Het gedrag mag gerust als een laagdoorlaat gezien worden. |
||||||||||||||
|
Beschrijving : |
||||||||||||||
|
Laag doorlaat, hoog doorlaat, bandsper en banddoorlaat. |
|
|||||||||||||
|
|
|
|||||||||||||
|
De afsnijfrequentie Fc is deze frequentie waarvoor het filter een verzwakking van 3dB (of 70,7 %) vertoont. |
||||||||||||||
|
In de doorlaat band kan een zekere "ondulatie" van 0,5 tot 1dB voorkomen. Meestal ondervinden we geen nadeel bij onze toepassingen. |
|
|||||||||||||
|
|
|||||||||||||
|
Bepaling van de in en uitgangs impedantie van het filter. |
|
|||||||||||||
|
Het aantal "cellen" vergroot natuurlijk de helling van het filter. Beide verzwakkingen (in en buiten de afsnijfrequentie) worden belangrijker. |
|
|||||||||||||
|
De frequentieband waarvoor de verzwakking tussen 0 en -3dB gelegen is. |
|
|||||||||||||
|
Opmerking : |
||||||||||||||
|
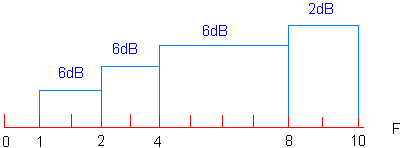
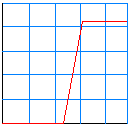
We spraken over de helling van de verzwakking uitgedrukt in dB/octaaf of dB/decade. Een tekening vervangt dikwijls een lange uitleg. Bekijk hieronder : |
||||||||||||||
 |
||||||||||||||
|
||||||||||||||
|
Samenstelling van het filter : |
||||||||||||||
|
|
|
|||||||||||||
 |
 |
|||||||||||||
|
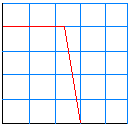
Op twee manieren kunnen we een laagdoorlaat filter bekomen. Beide schema's zijn even goed. Het bovenste zou wat gemakkelijker in gebruik zijn omdat er maar 1 spoel nodig is (hierdoor ook goedkoper). Tevens is de kwaliteitsfactor van een spoel moeilijker groot te maken. |
||||||||||||||
|
|
|
|||||||||||||
 |
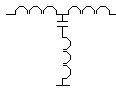 |
|||||||||||||
|
Meestal voor hoog frequent bedoeld. Het onderste schema steunt op de eigenschap van de serie resonantie. De impedantie is op dat moment zeer klein en sluit als het ware het signaal kort naar massa. De kwaliteitsfator bepaalt de verzwakking en de bandbreedte. Het bovenste schema is duidelijk. Op resonantie vertoont de parallel kring een zeer hoge impedantie en blokkeert het signaal. Buiten resonantie is de impedantie klein en de verzakking eveneens. |
||||||||||||||
|
|
|
|||||||||||||
 |
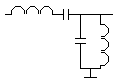 |
|||||||||||||
|
Je zou bijna zeggen: het wordt eentonig. Het hoogst getekende schema is een serie resonantie met zeer kleine weerstand op Fo. Buiten deze frequentie is de impedantie groot en wordt een grote verzwakking toegepast. Het andere schema is een combinatie van beide soorten resonantie kringen. Probeer de werking ervan te doorgronden. |
||||||||||||||
|
|
|
|||||||||||||
 |
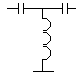  |
|||||||||||||
|
Voor hoge frequentie betekenen de spoelen een grote impedantie , enz.... Het zal wel lukken zeker ? |
||||||||||||||
|
Butterworth, Bessel, Chebyshev en nog andere... |
||||||||||||||
|
Dit deel is niet volledig en maar ter informatie. Dit zijn zijn namen van mensen die speciaal bijgedragen hebben geleverd aan de studie van filters. Voor laag of hoog doorlaat zijn de schema's gelijk maar de elementen onderling verwisseld. Natuurlijk zijn de waarden van de elementen bepalend voor de frequentie. De keuzen van het filter zal afhangen van wat men wenst te bekomen. Dieper ingaan op dit onderwerp zou ons te ver leiden. Zelfstudie met gebruik van goed naslagwerk is aangeraden. Hieronder ziet U een voorbeeld van het resultaat van de drie types filter. Het gaat om laagdoorlaat bestaande uit 5 elementen met een afsnij-frequentie op 3 db bij 50 Mhz. |
||||||||||||||
|
Een laag doorlaat volgens Butterworth curve met - Fc = 50 MHz |
||||||||||||||
|
|
||||||||||||||
|
Een laag doorlaat volgens Chebyshev met - Fc = 50 MHz |
||||||||||||||
|
|
||||||||||||||
|
Een laag doorlaat volgens Bessel met - Fc = 50 MHz |
||||||||||||||
|
|
||||||||||||||
|
Opmerking: Spoelen zijn onderdelen, meestal omvangrijk en moeilijk van goede kwaliteit te construeren. Men zal, daar waar mogelijk dit bouwelement door weerstanden vervangen. In hoger aangehaalde filters zal dat meestal het geval zijn. Denk even: 5 polig, zoveel spoelen. Men zou eerder het bouwen van filters opgeven. |
||||||||||||||
|
|
||||||||||||||
|
Filters vinden we zeker
terug aan de in en uitgangen van
zender/ontvangers. Dieper gaande studie is hier niet op de plaats. U wordt aangemoedigd om verder in deze materie Uw kennis uit te diepen. |
||||||||||||||
|
Naast de "klassieke" filters bestaan er andere types. We denken aan keramische en kwartsfilters. Het einddoel is steeds het zelfde. De manier om de werking na te gaan is identiek als bij de klassieke filters. |
||||||||||||||