De filters type RC - RL

Dit hoofdstuk maakt eigenlijk deel uit van wat direct vooraf ging. We behandelen nu het vervolg. Het werd reeds vermeld, spoelen zijn wat onhandig om mee te werken. Weerstanden kunnen mits oordeelkundig gekozen de spoel vervangen. Als je zegt RC dan houdt dat in dat RL ook bestaat. Afhankelijk van de plaats van de elementen zullen we een bepaald gedrag zien.
Een cel van RC :
Het samenstellen van R C filters is zeer eenvoudig (verbaasd ! ?). Zij zien eruit zoals hiernaast.
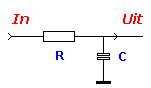Toetsen we dit filter aan de werkelijkheid. We gaan aan de ingang een wisselspanning aanleggen en de frequentie laten veranderen. Gelijk kijken we dan wat er aan de uitgang gebeurt.
De weerstand zal zich steeds als een weerstand gedragen en dit voor gelijk welke frequentie (laten we het technologisch probleem nu effe buiten beschouwing). De condensator , en dat weten we nu al, vertoont een reactantie omgekeerd evenredig met de frequentie. Bij stijgende frequentie vergroot de impedantie.	Extreem: bij oneindig grote frequentie is de impedantie (reactantie) NUL. Bij gelijkspanning is de impedantie oneindig groot.
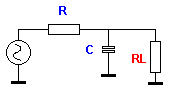	Bijgaand schema brengt ons naar de realiteit. Immers we moeten rekening houden met de belasting van het filter (anders kunnen we het niet gebruiken). RL is deze belasting. U merkt toch direct dat we te maken hebben met een spanningsdeler gevormd door de weerstand R en de condensator C (frequentie afhankelijk) waarover we de belasting plaatsen.
Bij lage frequentie is de reactantie van de condensator zeer groot. Gerust mogen we een open kring als resultaat nemen. Over de belasting RL komt de volledige spanning te staan maar volgens de spanningsdeler. Bij hoge frequentie zien we als het waren een kortsluiting. De kring wordt dan zwaar belast. Bij schakelen van RL (aansluiten van een volgende kring) levert maar een uitermate kleine spanning voor de volgende kring op. We hebben zeer duidelijk met een laag doorlaat kring te doen. Door de filter componenten van plaats te verwisselen bekomen we omgekeerde eigenschappen t.t.z. een hoogdoorlaat.	V e r z w a k k i n g
	Frequentie
Soorten van RC filters :
Reeds bekend: Laag -, hoog-, band doorlaat- en band sperfilters kunnen door een correcte keuze van de elementen bekomen worden.
Laagdoorlaat	Hoogdoorlaat
Afsnijfrequentie van een RC filter :
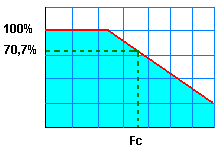	Hiernaast ziet U een verduidelijking van zo een filter. De afsnijfrequentie Fc is deze frequentie waarbij aan de uitgang nog 70,7 % van het volledige ingangssignaal overblijft. Dit is natuurlijk eveneens het geval voor een hoog doorlaat filter. Natuurlijk zal de belasting die we steeds zullen aansluiten van invloed.
De waarde van de afsnijfrequentie wordt door volgende formule bepaald: Waar in Fo in Hz R in Ω C in F
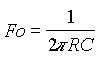U kan zich wel wat vragen stellen bij dat cijfer van 70,7 %. Bij filters is de waarde 3 db een veel voorkomende waarde. Men meet de uitgang bij veranderende frequentie tot we 3 db verzwakking bekomen. PM: 70,7 % is 1 gedeeld door wortel van 2 maal 100 om in procenten uit te drukken. We hebben hier met spanningen en niet met vermogens te maken.
Pijnig Uw hersenen eens en bestudeer de twee formules hier rechts: Beide komen met de 3 db overeen.
Een filter cel of pool RL :
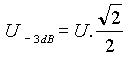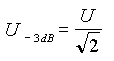Duidelijk moet zijn dat, eveneens filters bestaande uit weerstand en spoel eveneens bestaan. Het principe is het zelfde, enkel de plaats van de elementen werd aangepast.
Uw weet het zeker nog, Xl = Lω met  w = 2πf of reactantie van een spoel is recht evenredig met de frequentie. In het klaar: bij stijgende frequentie zal de reactantie evenredig stijgen. De spoel zelf heeft een laagdoorlaat gedrag bij grotere frequentie. (trouwens, omgekeerd als bij een condensator)
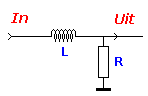
Laagdoorlaat	Hoogdoorlaat
Uw kan de uitleg van de werking zelf al bepalen. Voor wie het nog niet duidelijk is: Bij lage frequentie (laag is betrekkelijk) is de reactantie klein en extreem nul. Het volledige signaal zal over de weerstand terug te vinden zijn. Bij vergroten van de aangelegde frequentie zien we door het vergroten van deze impedantie een kleiner deel op de uitgang. Duidelijk is dat het laag doorlaat effect te zien is.		Omgekeerde werking maar hier laat ik de uitleg volledig aan Uw zorgen over. Een duidelijk hoogdoorlaat gedrag, toch?.
Afsnijfrequentie van het RL filter :
De uitleg loopt parallel aan deze van een RC filter. De afsnijfrequentie FC is deze frequentie waarvoor de uitgang nog 70,7 % van wat aan de ingang staat, bedraagt. Het 3 db punt is ook hier van toepassing. Enkel de formule zal omdat complementaire elementen gebruikt worden er anders uitzien.
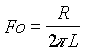		Met R in Ω F in Hz L in H
Zoals voor de RC cel wordt de spanning op 3 db op een zelfde wijze bepaald.
of
Hoe komen we tot deze formule ?
Het is nuttig hier overweg mee te kunnen voor als U de formule vergeten bent.
De afsnij frequentie is deze waar voor de reactantie gelijk aan de weerstand is (spoel of condensator)
Met andere woorden: als Xc = R weze   1/Cω = R    (met ω = 2πf) of RCω = 1  wat equivalent is met 1= RC2πf of f= 1/RC2π Op een zelfde wijze herhalen we voor RL: Xl = R weze Lω = R    (met ω = 2πf) of L2πf = R of f = R/2πL
We gaan nog wat dieper (niet echt nodig voor het examen)
Hoe de verzwakking berekenen bij een bepaalde frequentie ?
Nog maals, het filter bestaan uit een spanningsdeler waarvan een element frequentie afhankelijk is. We gaan nu wat rekenwerk in de diepte doen.
Verhoudingen van spanning in / uit gebeurt volgens proportionaliteit. De verhouding van spanningen is dezelfde als de verhouding van de reactantie met de impedantie van de kring.
Door nu de impedanties in rekening te brengen (regel van Pythagoras)
In ons voorbeeld gaan we één en ander uitrekenen voor de bijzondere toestand dat X = R is, (reactantie gelijk aan de weerstand van het filter). Ik geef toe , een lange draad:
Nog, de verzwakker van dit filter ?
Dit soort filter verzwakt 6 db per octaaf. Ook dit hebben we reeds gezien in het voorgaande hoofdstuk. Ter verduidelijking: indien we een filter met een verzwakking van 10 db bij 10 khz hebben, dan is de verzwakking bij 16 db op 20 khz (het dubbele of een octaaf). Indien een nog grotere verzwakking vereist is moet men maar meerdere elementen in serie plaatsen. Niet direct eenvoudig want de volgende kring belast telkens de voorgaande en laat zijn invloed gelden.
Tot zover de Rc, RL filters.