De decibel

Dit is de eenheidsmaat die we dagelijks zullen gebruiken. Zoals meestal werd dit ingevoerd om de zaken te vereenvoudigen. Op reklame van radio of andere electronische communicatie toestellen zullen we deze term veelvuldig tegenkomen. Effe doorbijten om deze stof onder de knie te krijgen. Voor diegenen die het wiskundige niet zien zitten hoeven niet af te haken. Een minumum kennis en memorizeren van specifieke waarden kunnen volstaan. Toch maar proberen van maximaal wat op te steken.
Zoals de naam doet veronderstellen is de decibel een tiende deel van de BEL. Graham Bell heeft deze term ingevoerd. Om een en ander te begrijpen is het nuttig om er wat wiskunde bij te halen. Het kan afschrikken maar doorbijten en het zal wel loslopen. Sommige onder ons zullen uit hun schoolverleden zich het werken met logarithmen kunnen herinneren. Daar gaan we.
Zonder dat U het weet heb je een zintuig dat het geluid volgens de logarithmische regel meet . Dat is het gehoor. Een verdubbeling van geluidsvermogen geeft ons niet de indruk op het gehoor, dat we dit geluid als dubbel sterk ondergaan. Het is pas als het geluidsvermogen 10 maal in vermogen stijgt dat we een indruk van een verdubbeling merken. Electronische geluidversterker is een voorbeeld dat misschien beter ons dit effect doet inzien. De fysiologische indruk volgt deze regel. (let, het gaat hier om een enkele frequentie van geluid, voor meerdere geluidsbronnen met ver uit elkaar liggende frequenties is dat niet het geval)
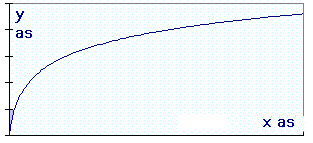U ziet hierboven een curve volgens een logaritmische regel. Voor de duidelijkheid: de waarde "x" evolueert veel sneller dan de waarde volgens de "y" as.	Deze voorstelling zou er een kunnen zijn van Uw gehoor. Op de "x" as vinden we de evolutie van het geluidsvermogen. Op de "y" as zien we de fysiologische indruk.
Notatie :
Omdat we nu eenmaal 10 vingeren (of tenen) hebben, zijn we sedert onze kindertijd gewoon om de cijfers op basis 10 te gebruiken (0,2,3,4,5,6,7,8 en 9). Moest dit niet zo zijn dan had de mens waarschijnlijk een ander basis aanvaard (en mogelijk maar zeven vingers , haha). Bijgevolg is het niet vreemd dat er inderdaad andere basissen voor getallen kunnen bestaan. Het zelfde kan gezegd voor het logarithme. We zien bv:
Het log van het natuurlijk getal "e". Men noteer dit als ln. Dit is de enige referentie. Hoe we overgaan tot het logaritme in basis 10 zien we verder.	e= 2,72 ( benadere waarde, tiendelig)
Omdat we dat nu eenmaal gewoon zijn gebruiken we in de radio electriciteit de basis 10. De overgang ziet U in wat volgt : Bemerk tevens de aanduiding log voor basis 10
ln X Log (10) X =________                         ln 10	We duiden dit als volgt aan: Het logarithme in basis 10 is de verhouding van het ln log van dat getal en het ln (basis) van 10
Nogmaals, merk het verschil van aanduiden volgens het basis getal.
Voorbeeld : Bereken het log basis 10 van het getal 1000:
Vul in :                             ln 1000            6,9077 Log (10) 1000 = _______= __________      = 3                                  ln 10            2,30025
Een meer gebruikte manier om het logaritme te begrijpen is: Het logaritme van een getal in basis 10 (als vb) is dat getal waarvoor men het basisgetal tot de macht moet verheffen om dat getal te bekomen. Het zelfde voorbeeld: Het logaritme van 1000 is dat getal vaartoe men het basis getal moet verheffen om dat getal te vinden. Dus log 1000 (in basis 10) is 3 daar 10 tot de macht 3 is 1000. Effe wennen maar niet zo moeilijk.
Waarom het ons moeilijk maken en de decibel gebruiken?
Als we teruggaan naar ons gehoor of akoestisch probleem dan weten we dat voor zeer lage niveau's er een moment komt dat wij niks meer horen. Men zegt dat de accoustische druk onder de gevoeligheidsdrempel van ons gehoor daalt. Gemiddeld kunnen we dit stellen op ongeveer20.10-6 Pa (eenheid van druk). Omgekeerd , de maximum druk die we nog kunnen verdragen zonder dat er direct schade aan ons gehoor wordt berokken is rond de 200 000 000 10-6 Pa. De verhouding tussen deze twee waarden kunnen we gerust stellen op minstens 10 000 000, geef toe dat deze cijfers moeilijk te hanteren zijn. Daarom, doen we de berekening volgens het log dan vinden we een verhouding R = 7 wat ons toelaat te zeggen dat de verhouding tussen beide minima en maxima gelijk is aan 7 Bel
Van waar de uitdrukking db ?
Juist hierboven hebben we gezien dat 7 Bel een verhouding van 10 000 000 vertegenwoordigt. De Bel is een te grote eenheid. Het is gemakkelijker dat een kleinere onderverdeling zou gebruikt worden. De decibel is een tiende van de Bel. In ons voorbeeld kunnen we 7 Bel schrijven als 70 db, beter en toch eenvoudig, niet ?
De decibel (db) toegepast bij radio :
Verhoudingen van waarden toegepast in radiotechniek kunnen we vergelijken met wat bij het geluid gebeurt. Beter nog , verhoudingen tussen signalen van meer dan 70 db zijn geen uitzonderingen maar eerder regel. Er is nood om versterking of verzwakking uit te drukken en 20 db is gemakkelijker dan een versterking van 100 (voor spanning). Bovendien is er nood om versterkingen en of verzwakkingen te combineren en dan is het eenvoudiger werken door optellen van db dan dat we gaan vermenigvuldigen. Ronde getallen als 100 maal terzijde gelaten. Ook is het nodig om vermogens uit te drukken ten opzichte van een vaste referentie waarden. U voelt het, men ontkomt er niet aan. U zal het merken, bij gebruik van meettoestellen praat men over niets anders.
Definities :
In vermogen De dB is 10 maal het log (basis 10) van de verhouding vermogens   P1/ P2.	P1 dB = 10 Log   ______                       P2
Met spanning De dB is 20 maal het log (basis 10) van de verhouding spanningen   V1/ V2. De spanning V staat volgens het kwadraat naar vermogen maar wel bij gebruik van identieke weerstandswaarde.	V1 dB = 20 Log   ______                       V2
Voorbeeld  1 : Wat is de versterking in vermogen in db van een versterker waaruit 20 W voor 1 W aan de ingang komt ?	20 A =   10 Log  ______  =   13 dB                       1
voorbeeld 2 : Wat is de verzwakking in vermogen van een verzwakker in db uitgedrukt als 100 W ingang herleid wordt toto 15 W ?	15 A =   10 Log  ______  =    - 8,2 dB                       100
Voorbeeld 3 : Welk is de versterking in db van een transistor als men 10 mV aan de basis koppeld en er 3 V op de collector verschijnt ?	3 A =   20 Log  ______  =   49,5 dB                       0.01
Nota : Wees ervan verzekerd dat NOOIT eenheden gemengd gebruikt worden. Het is uit den boze om spanningen met vermogens te vergelijken zonder de nodige omzetting vooraf te doen.
Enkele eigenschappen van logaritmen : (eindelijk wat wiskunde)
Log ( A x B) = Log (A) + Log (B) Log ( A/B) = Log (A) - Log (B) Als Ab = C dan  log(a) C = B   ( 102 = 100 equivalent aan Log (10) 100 = 2 ) log Ab = B x log A
Een praktische toepassing uit de radio electronica :
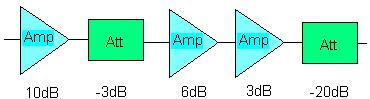De tekening hierboven geeft een samenstelling van versterkers en verzwakkers weer. Zulke dingen komen in de praktijk frequent voor. We denken aan onze zender gevolgd door een verzwakking door de aanpassing en kabelverlies enz... Als we deze waarden kennen is het eenvoudig om het eindresultaat te beplalen.
1 ste geval in dB: +10 - 3 +6 + 3 -20 = -4dB voor het geheel zien we dat er een verzwakking van het signaal optreed. 2 de geval volgens verhouding van vermogens 10 (keer)  x 0,5 x 4 x 2 x 0,01 =  0,4 (keer) eenvoudige controle door de berekening in :  10 Log 0,4 = 4 dB
Algebraïsch optellen komt ons veel eenvoudiger dan vermenigvuldigen voor. De verzwakking van een coax als men deze per eenheidsmaat (vb per 100m) is niet ingewikkeld om te bepalen. Natuurlijk is de kennis van de juiste lengte noodzakelijk.
De omgekeerde bewerking, we kennen de dB waarde maar wensen de verhouding te kennen ?
Het is zoiets als met de € (Euro) en de frank. De verhouding van vermogens spreken meer aan (voor sommige toch). A (db) de waarde in dB R de verhouding van vermogens P1/P2	Meerdere oplossingen kunnen gevonden worden. Zonder er diep op in te gaan tonen we hier twee. Het resultaat telt.
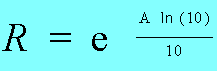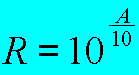In de formule hierboven maken we gebruik van het natuurlijk log , Ln. het basis getal is e. Voor de berekening moeten we gebruik maken van het tiendelig stelsel.	Deze formule is duidelijk eenvoudiger.
We gebruiken de tweede oplossing en voeren de gegevens in een calculator in. Bijvoorbeeld : wat betekend 23 db. R =  10 tot de macht 23/10    weze 10 2,3 = 200 niet erg ingewikkeld toch ?
Een tabel met veel gebruikte waarden kan handig zijn. (in vermogens): in het rood, de belangrijkste waarden
Verhouding dB Verhouding dB Verhouding dB Verhouding dB 1 0 20 13 100 20 1000 30 2 3 25 13.98 150 21.76 2000 33 3 4.77 30 14.77 200 23 3000 34.77 4 6 35 15.44 250 23.98 4000 36 5 6.99 40 16 300 24.77 5000 36.99 6 7.78 45 16.53 350 25.44 6000 37.78 7 8.45 50 17 400 26 7000 38.45 8 9 55 17.4 450 26.53 8000 39 9 9.54 60 17.8 500 27 9000 39.54 10 10 65 18.1 550 27.4 10000 40 11 10.4 70 18.45 600 27.78 20000 43 12 10.8 75 18.75 650 28.13 30000 44.77 13 11.14 80 19 700 28.45 40000 46 14 11.46 85 19.3 750 28.75 50000 47 15 11.76 90 19.54 800 29 100000 50
Bij het lezen van electronica lektuur vinden we dikwijls volgende of gelijkaardige uitdrukking terug: De doorlaatband van een versterker op 3 db bedraagt 4 Mhz. De punten op de doorlaatband versterking in db volgens de frequentie hoger gelegen dan 3 db of een verhouding van twee.	Het deel gelegen tussen deze twee punten wordt doorlaatband genoemd. We zien dit bij de antennes, versterkers , enz... Het moet duidelijk zijn dat men goed moet uitkijken dat men winsten in vermogens niet met winst in spanning door mekaar mag gebruiken. 3 db betekend een verhouding 2 in vermogen maar 1,41 of wortel 2 in spanning . Dit is eveneens voor stroom waar.
De dBm :
Een variante op het reeds geleerde, de decibel in verhouding tot milliwatt. Het is confortabel om een gemeenschappelijke referentie te gebruiken. De mW is zo een voorbeeld. Natuurlijk moet als we hier over vermogens spreken de impedantie waarover dit gebeurt identiek gehouden worden. Een voorbeeld is de 50 Ω zoals veel voorkomt op radio HF. U moet degelijk het verschil merken als gebruik gemaakt worden van belastingen van 75 Ω zoals in TV. 0 db is voor beide gevallen verschillend. 0 dBm op 50 Ω = 224 mV in een belasting van 50Ω = 1mW 0 dBm op 70 Ω = 224 mV in een belasting van 70Ω = 0,7mW Wat is de bruikbaarheid ? Vergelijken van gevoeligheid van ontvangers is duidelijker als men gebruik maakt van gemeenschappelijke referenties. Als we bij zenders de uitgang in dbm kennen en alle verzwakkende elementen zoals verliezen (coax, pluggen, afstanden , ontvangst parameters enz... ) is het met meer precisie dat ontvangstmogelijkheid op een bepaalde afstand tegeëvalueren. Een voorbeeld : uw signaal bij uw correspondent is -120 dBm , u zorgt ervoor dat uw vermogen groeit met 4. Dit komt neer op een verhoging van 6dB (zie de tabbel hierboven), uw signaal van oorspronkelijk -120 dBm gaat naar -114 dBm bij uw correspondent. mooi toch ?
Berekening :
U kent het vermogen P in milliwatt: dBm  = 10 Log P	U kent het vermogen P in watt: dBm  = 10 Log P . 103
dBm 0 10 20 30 40 50 60 70 W 0,001 0,01 0,1 1 10 100 1000 10000
Overgaan van dBm in milliwatt of naar watt :
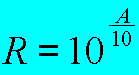	Zoals steeds (haha!) volstaat het de formule toe te passen. R = Vermogen in milliwatt A = dBm
Voorbeeld: We beschikken over een vermogen van 20 dbm, wat hebben we dan in mW ? R =  10 tot de macht 20/10 , of 102  = 100 mW
De dBW:
Het zelfde principe blijft natuurlijk van toepassing maar we drukken nu het vermogen in Watt uit. Afhankelijk van de grootte van het aanwezige vermogen gaan we Watts of milliWatts gebruiken.
U ken het vermogen in watt (als P) dBW  = 10 Log P
Wetenswaardig de dBi en dBd :
Fabrikanten spelen graag met zulke termen (om indruk te maken ? of keuzes te beïnvloeden ?). Rede om het onderscheid tussen al die db 's te kunnen maken.
Bij dbi staat de i voor isotropisch en zien we deze term terug wanneer het gaat om een idee te geven van de winst van een antenne. Isotropisch wil zeggen dat de straling van het electromagnetisch veld gezien wordt vanuit een enkel punt (in ALLE richtigen evenredig uitgestraald). Dit soort antenne is een theoretisch model en bestaat in de werkelijkheid niet.
Daartegenover staat de dBd waarvoor de referentie de dipool is. We gaan het nog zien, de dipool is De basis antenne waarvan alle andere afgeleid werden. Het idee is logisch om zich naar de halvegolf antenne (dipool) te wenden, maar het ware beter dat slechts EEN referentie gebruikt zou worden. Maar ja....?
Een voorbeeld om het verschil te laten zien:
Zoals U zal merken is het verschil niet te verwaarlozen. Een leek zou zichzelf kunnen laten misleiden. Een antenne met 10dBd als winst met referentie naar de dipool heeft een winst van 12.15 dBi waarbij de energie isotropisch gestraald wordt. Welke zou U kiezen? Bij publiciteit over antennes is de verleiding reëel om enkel de notatie db (zonder d of i) de zaken wat mooier voor te stellen. U bent verwittigd.
De dBc :
Het is ook nuttig om aan deze term hier wat aandacht te besteden. De klein "c staat voor "carrier" in het Engels of drager zoals wij dat zeggen. Men maakt ook hier een vergelijk van vermogens maar nu van een complex signaal met een bepaalde bandbreedte. Het zou kunnen gaan in verband met harmonische van deze "carrier" of samenstelling van een signaal. We zagen het reeds , zulke signalen vragen een bepaalde breedte van het spectrum teneinde met minimale vervorming doorheen een kring te kunnen gaan. Anders uitgedrukt, de kring moet rekening houden met het signaal (bandbreedte) en niet omgekeerd. Het is ook hier onontbeerlijk dat de wijze van vergelijken op een eenvormigen manier gebeurt. Om een en ander te verduidelijken maken we van nevenstaande figuur gebruik. Een signaal met een bepaalde bandbreedte is samengesteld door de "carrier" en om een idee te geven van de benodigde bandbreedte hebben we twee punten op de frequentieas genomen. Het volstaat om eenduidig te zijn en deze twee punten (frequenties) te defineren als die frequenties waarvan de amplitude gereduceerd wordt tot een overeengekomen waarde vb: 3 db. 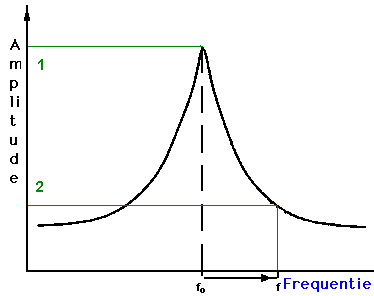Dus: Fo is de drager of "carrier" , f is in ons voorbeeld de hoger gelegen frequentie van het samenstellend signaal waarvan de amplitude bv: 3 db minder groot zou zijn. Een zelfde punt vinden we voor een lager gelegen punt. De notatie "amplitude " kan zowel op spanningen als op vermogen slaan. Uw moet zelf nu in staat zijn om dat onderscheid te maken. De frequenties bepaald door de twee punten bepalen de bandbreedte op 3 db ten opzichte van de drager "carrier" vandaar dbc , notatie die , we moeten het stellen, niet zoveel gebruikt wordt.
Omzetting/dB Spanning- Stroom /dB
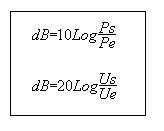
Invoer van gegevens Waarde 1 =         De waarde 1 verwijst naar de uitgang, de waarde 2 stelt de waarde aan de ingang voor. Waarde 2 =     Resultaat:    dB	Wat U moet onthouden: indien het resultaat negatief is dan gaat het om een verzwakking. Daartegenover is het resultaat positief bij versterking Tevens de twee formules hoger...
Persoonlijk hecht ik veel belang aan dit hoofdstuk. U zal veelvuldig geconfronteerd worden met BEL en DB. Ook nuttig is om bepaalde standaard waarden uit het geheugen te kennen. Herneem hiervoor de waarden in het rood vermeld in hoger staande tabellen. Let vooral op het feit dat vermogens en spanningen of stroom wat ander cijfers opleveren. Succes !!!!

Terug naar RCL Home page.

Bewerking : ON4AWN, Herman Van Meerbeeck