Beschouwingen betreffende ontvangst

Ontvangen van radios signalen is ingewikkelder dan zenden. We gaan proberen om enkele basis informatie mee te geven. We hopen dat achter de cijfers die gepubliceerd worden er minder vraagtekens zullen overblijven.
Stel U hebt pas zo een hyper modern Oosters toestel aan geschaft. Uw oud toestel dreigt onder het stof te verzijlen. Gelukkig heb je de reflex om dit glimmend toestel toch maar een laatste maal met het oude te gaan vergelijken.	De verwachtingen staan hoog. Jaja, had je dat maar niet gedaan is een eerst mogelijk reflex. Het valt tegen. De kwaliteit valt tegen, het toestel ruist meer en de klank lijkt minder kristal helder. Dit verhaal hoeft niet direct steeds zo te zijn. Maar toont het belang om toch wat dieper in die technische jargon van specificaties te gaan...
Basis notatie : RUIS
20 ° warmte in huis, mooi. Maar als we zeggen dat we leven in een temperatuur van 273,.. °C, dat klinkt anders maar is ook correct. Het kan kouder. theoretisch zou men tot -273,15 °C kunnen dalen.	Deze temperatuur noemt men "het absolute nulpunt" of vergeleken met de voor ons meer gangbare notatie: -273,15 °C. "KELVIN" is de man aan de basis van dit verhaal.
Men kan eenvoudig van een notatie naar de andere gaan. : K = C + 273, 15 C = K -  273,15	Voorbeeld: 20 °C in graden °K ? 20 + 273,15 = 293,15°K
Bij 0 °K zijn ALLE therische bewegingen volledig stil gevallen. Immers onder invloed van themperatuur bewegen de elementaire bouwstenen van alle stoffen stochastisch. Naarmaten men koelt wordt energie aan die bewegingen ontrokken. Dit maakt dat eens alle bewegings energie weg genomen het niet meer mogelijk is om nog in temperatuur te dalen. Deze toestand wordt bij - 273,15 °C of 0 °K bereikt.	U kan zich best voorstellen dat bij 293,15 °K of 20 °C deze bewegingen aanzienlijk zijn. Deze bewegingen liggen aan de basis van RUIS. Als proef: sluit een 50 Ω weerstand aan de ingang van Uw nieuwe blinkende ontvanger. U hoor RUIS van verschillend niveua als U de vergelijking maakt met Uw oud toestel meer of minder laten we buiten beschouwing. RUIS ontstaat door die thermische bewegingen IN de weerstand. Ja , je hebt gelijk, steek Uw toestel in de diepvries en je zal wel minder ruis horen. Niet praktisch maar soms wordt naar deze technieek gegrepen voor bijzondere toepassingen.
Pech, maar de realiteit. Alle in onze toestellen gebruikte componenten zijn aan dit fenomeen onderhevig. Men stuit dus op een niet overschreidbare limiet wat ruis aangaat. Weerstanden, draad , condersator, enz... allemaal plezier verbroddende elementen, maar het kan niet zonder. Maak er dan maar het beste van door oordeelkundig met die dingen om te gaan. Wist U dat RUIS (witte in dit geval) therapeutisch voor het gehoor kan werken. Bij witte ruis zijn ALLE frequentie gelijkmatig aanwezig in het audio spectrum en bijgevolg voor de mens van geen betekenis. Filteren leveren "roze" , "bruine" en ander soort ruisvarianten.
Kwantificatie van RUIS (thermisch):
Het gaat over een beroemde formule. Voor een bepaalde bandbreedte (in SSB is dat 2400 Hz) en een gegeven temperatuur ontstaat een zeker ruisvermogen.	P = k T B
	P = vermogen in Watt k = constante van Boltzmann 1,38 10-23 B = doorlaat band in Hz T = temperatuur in °K (Kelvin)
Het ruisvermogen gaat evenredig met de temperatuur. Merk tevens dat de waarde van het element (hier als voorbeeld de weerstand) geen invloek uitoefend.
Voorbeeld : We gaan het ruisvermogen in een weerstand onder omgevings temperatuur berekenen (20 °C) voor een doorlaatband van 2400 Hz.	Dit geeft ons: P= 1,38 10-23 x 2400 x 293 = 9,7 10-18 W
Wel een wat moeilijk formaat om mee te werken. Daarom gaan we een omzetting doen naar de milliwatt en in db. of dbm. Een mw = 0dbm komt overeen met 220 mV over 50 Ω.	PdBm = 10 Log ( 9,7 10-15 ) = -140 dBm vergeet de aanpassing W naar mW niet.
Waartoe dient dat? Eenvoudig , we berekenen het vermogen van de ruis door thermische agitatie bij een gegeven temperatuur. Het signaal op onze antenne als voorbeeld beschikt eveneens over een bepaald vermogen bij ontvangst maar ook ruisvermogen eigen aan het thermisch effect.	Onder gegeven omstandigheden zal , bij radio trafiek, er aan de ingang van onze ontvanger een natuurlijk ruisniveau ontstaan van 140 dbm (zoals in een weerstand). Een signaal op de antenne kleiner dat deze waarde zal in die ruis verdwijnen en dus niet meer leesbaar zijn. 140 dbm is het niveau ZONDER antenne aangesloten.
Dit is belangrijk om te begrijpen. Er is een fysische beperking aan de gevoeligheid van ontvangers en deze beperking wordt onder anderen door dit natuurlijk fenomeen verbonden aan temperatuur gedicteerd.
Bestaat er andere vormn van ruis ?
Onze wens gaat niet in vervulling, ja dus. Hierboven aanzagen we de ontvanger als volledig van de buitenwereld geïsoleerd. Dit is natuurlijk niet het geval. Om wat te ontvangen moeten we een antenne aansluiten. De buiten wereld die we door het aansluiten van de antenne binnen brengen is van meerdere oorsprong. Bekijken we nu enkele bronnen.
RUIS door de mens veroorzaakt (Man Made Noise). Iedereen is daar schuldig aan. Telkens U een toestel (elektrisch) aanzet veroorzaakt U gratis ruis. Ook motoren in wagens en andere zijn schuldig aan deze misdaad. De concentratie is logischerwijs direct evenredig aan het resultaat van ruis. Sparen maar en op de buiten wonen. Atmosferische ruis. De mens zal het klimaat nog niet snel kunnen beïnvloeden of bepalen. Onrechtstreeks is de zon de moter van ons klimaat en dus ook van de produktie van een deel van de ruis die ons verveelt. Luister maar eens naar radio tijdens een onweer (onweer... zelfs op grote afstand). Steeds zijn er wereldwijd natuurlijke fenomenen die ruis produceren.i Galactische ruis (klinkt futuristisch). Vooral VHF/UHF maar ook decametrische banden lijden hier onders. Ook de zon is schuldig maar in tegenstelling van een indirecte invloed via de athmosfeer gaat het om directe onder de vorm van straling vb gamma stralen om er een te noemen. Een andere benaming is comsmische straling. Uw weet dat er bijna oneindig veel zonnen in de kosmos bestaan en die allemaal wat bijdragen. Gelukkig niet oneindig want dan zou de straling ook oneindig zijn. Op 2 meterband kan je een verschil merken als je een richtantenne naar de zon keert en daarna ervan weg, merk het verschil.
Waarop baseert men zich om de gevoeligheid van een ontvanger te bepalen?
De gevoeligheid is de bekwaamheid van een ontvanger om voor een gemoduleerd signaal aan de ingang , een wel bepaald LF signaal voor te brengen. Des te kleiner dat ingangs signaal des te gevoeliger deze ontvangen.
Bepalen we dit onder de vorm van cijfers:
De gevoeligheid van de ontvanger is enkel afhankelijk van de ruisfaktor We hebben gezien dat er een grens voor de gevoeligheid bestaat en dat ontvangst onder deze grens niet mogelijk is. De werkelijkheid is dat ontvangers meestal deze grens zelfs NIET halen.	Door zijn constructie zal de ontvanger steeds wat ruis bijdragen. Het verschil tussen de theoretische waarde en de werkelijke noemt men de ruisfaktor welke in dB uitgedrukt wordt. Een snelle berekening zal wat meer licht op de zaak brengen.
De theoretische ruis die we hierboven voor een signaalband van 2400Hz modulatie berekend hebben voor een temperatuur van 20 °C is onze referentie waarde. We hebben hiervoor -140 dBm.	Indien onze ontvanger een ruisfaktor bezit van 6 dB betekend dat dat een signaal van -140 + 6 = -134 dBm zal nodig zijn om opgemerkt te worden.
Hierboven ziet U grafisch wat verduidelijking. We gebruiken tevens de reeds vernoemde cijfers (6 dB en -140 dBm). We merken duidelijk dat als aan de ingang er signaal verschijnt dat groter is dan -136 dBm het signaal leesbaar zal zijn. Voor waarden onder deze zal dat niet het geval zijn. Merk toch op dat 0dBm eigenlijk wel een grote waarde betekend. Vb: -115 dBm is een fors signaal (20 dB boven dat minmum signaal of 100 maal groter).
De correcte ruisfaktor van de ontvanger: (interpretatie)
We moeten rekening houden met de frequentie banden waar het ons om gaat. Decametrisch is de uitwendige ruis uitermate hoog (meestal toch). Daarom is een overdreven kwalitatief ontvanger (op ruis gebied) niet strikt nodig. (eerder het tegendeel)	Op de band 3,5 Mhz is een ruisfactor niet direct een nadeel. Bij steigende frequentie zal de ruisfaktor verminderen. De praktijk zegt ons dat een ruisfaktor van 15 dB voldoende is, de rest (beter of kleinere faktor) zou enkel ruis leveren. Deze vooropgestelde waarde is zeer realistisch.
Een ander verhaal is voor VHF geldig. Door de daling van het niveau van uitwendige ruis, wordt het wel interessant om die ruisfaktor zo klein mogelijk te maken. Alles heeft zijn neveneffecten. Zonder voorzorg kan het wel eens gebeuren dat in de versterker trappen vooraan er saturatie, kruismodulatie enz.. optreden. Dus opgepast zeker ook niet teveel voorzersterken.	Heden ten dagen bereiken moderne voorversterker 0,2-0,3 dB als ruisfaktor wat opzich opmerkelijk is. Vestig Uw aandacht op het enorme verschil tussen HF en V/UHF ontvangers en laat U niet misleiden door gegevens vervat in technische folders of reklame.
We denken terug aan de formule P=ktB en merk dat de temperatuur een belangrijke invloed heeft. Indien we de ruisfaktor willen verkleinen kunnen we de versterker in de diepvries steken wat duidelijk niet praktisch is. Schrik niet , het is omdat wij amateurs niet zo ver willen gaan dat vooral in militaire omgeving men tot die oplossing kan komen. Gebruik van cryogeen techniek. Wat vrediger, radio astronomie, waar de budgetten het toelaten gaan ook deze techniek toepassen.
Een voorbeeld van ontvanger:
In een ontvanger vinden we passieve elementen (weerstanden, spoelen...) en aktieve (versterkers enz...). Elk onderdeel is verantwoordelijk voor verlies of winst. Elke versterker heeft zijn eigen ruisfaktor en winst.	We stellen voor elke trap van versterkers de winst G en zijn ruisfaktor F vast. We kunnen volgend verhaal schrijven. Winst en ruisfaktoren worden in dB uitgedrukt. Maar kunnen ook als verhoudingen bepaald worden. (vb: 6dB is een verhoudig van 4 en 3dB is er een van 3 en 10 dB geeft ons 10)
	F2-1           F3-1           Fn-1 F= F1 + ____   +   ______  + _________                 G1             G1 G2        G1 G2 Gn
Uit dit ziet U dat voor de totaal ruis faktor de eerste versterkertrap van de keten bepalend is. Dus die eerste trap moet zijn ruis faktor het kleinst zijn.	Het berekenen van de winst van een passief element (filter als vb) door toepassing van:              1 G =  _________              F Voorbeeld : een filtre met 3 dB verleis Zijn ruis faktor is 3 dB of een verhouding = 2 en zijn winst zal 1/2 = 0,5.
Voorbeeld :
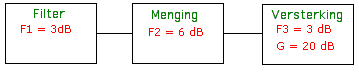In dit voorbeeld hebben we een filter met 3 dB invoegings verlies, een mengtrap (passief of geen versterking) met een verlies van 6 dB, gevolgd door een versterker met 20 dB winst en een ruis faktor van 3 dB. De manier van werken
Berekenen we eerst de ruis faktoren en de winst van elk onderdeel en dit niet is dB maar in verhoudingen. Filter : F1 = 3dB een verhouding van 2 dus F1 = 2           G1 = 1/F1 = 1/2 = 0,5  dus G1 = 0,5 Mengtrap : F2 = 6dB of verhouding 4 dus F2 = 4                   G2 = 1/F2 weze 1/4 = 0,25 dus G2 = 0,25 Versterker : F3 = 3 dB of een verhouding 2 dus F3 = 2            G3 = 20 dB verhouding 100   dus G3 = 100 De formule nu :                   F2 - 1                      F3 - 1 F = F1 +  ____________    +   __________                    G1                         G1 G2                   Wat in dB : 10 Log (16) =  12 dB betekent
Ruis faktoren vindt men zelden in publiciteiten
Meestal wordt op volgende manier de parameter ruis in rekening gebracht. De gevoeligheid 0,5 µV voor 10 dB de (S+R)/R (Sig + ruis, gedeeld door de ruis), zegt wel wat maar niet veel. We kunnen wel de omrekening doen door die 0,5 µV signaal over de 50 Ω te herekenen naar vermogen. Berekening van het vermogen : Merk het terug brengen naar mW om gemakkelijker verder te werken. in dBm :  10 Log (5 10-12 ) = -113 dBm De opgegeven waarde was 10 dB de (S+R)/R , dus S/R +1 = 10 en dus   S/R = 9 il vient De som (-113 -9 = -122 dBm). Het ruisniveau (optimaal) voor een bandbreedte van 2400 Hz is -140 dBm en hieruit leiden we dan de ruisfaktor af van de ontvanger = -140 - (-122) =  18,   wat ons op 12,5 dB brengt.
Men hoort er over of men stelt het zelf vast, bij het luisteren verdwijnen vervelende signale als ik de ingangsverzwakker inschakel. !!
Men heeft er meestal baat bij om dit onderdeel oordeelkundig te gebruiken (wat zeker niet steeds het geval is). Indien U veel last hebt van storende signalen in de omgeving van dat wat door gewenst te ontvangen dan zal U merken dat door het inzetten van de verzwakker of zelfs een attenuator het Uw leven heel wat aangenamer maakt. Signalen verzopen in ruis en/of stoor signalen komen plots veel beter tot uiting. Intermodulatie speelt U minder parten.
	Bekijk het signaal hiernaast als voorbeeld. Wat gebeurt er. Merk het station op 7050 kHz en een ander op 7060 kHz. Tot zover niks abnormaal. Stel (en het komt meer voor) dat twee signalen sterk aanwezig zodat Uw ingangs versterker gesatureerd wordt. Spijtig maar U zal merken dat hier intermodulatie optreedt. Het samenspel fabriceert signalen die eigenlijk niet aanwezig zijn.
De producties hebben volgende waarden : 2F1 - F2 en 2F2- F1 (en tevens 2F1+F2 en 2F2+F1 maar deze vallen buiten ons gehoor), Men noemt hen van de derde orde  = (2+1 ou 2-1 (coëficienten)). We rekenen: (2*7050)-7060 = 7040, en (2*7060)-7050 = 7070 kHz. Dit zijn de opgewekte signalen.	Dit brengt ons er toe dat we spreken over het interceptiepunt. De laatste jaren zien we deze parameter wel op de reklame folders.
Interceptie punt of interception point :
Naast het feit dat het voor de publiciteit mooi klinkt , wat betekend dat nu voor ons?
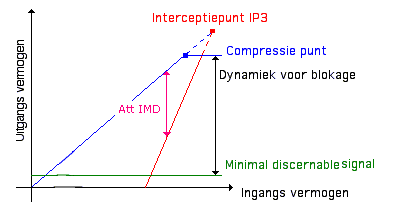
Zeker geen eenvoudige stof en niet onontbeerlijk voor het examen. De figuur hierboven zal wel duiderlijker worden als U dit hoofdstuk heb doorgenomen. We onderzoeken het uitgangsvermogen volgens het antenne signaal. De blauwe lijn vertegenwoordigt het verloop van een normaal signaal aan de antenne. In ons voorbeeld lijkt het verloop aardig lineair. Op een gegeven ogenblik merkt U een kink in dat veloop. Het LF stijgt niet meer volgens een stijgend antenne signaal. (een soort verzadiging). Men noemt dit punt "Interception point" (in het Engels). De rode lijn is een ander verhaal. Het geeft het verloop van het intermodulatie produkt van derde orde. (2f1-f2 en 2f2-f1) . Merk dat het verloop veel steiler is dan de blauwe lijn. Weet dat dit signaal werd veroorzaakt door de versterker in ons geval.
Het interceptie punt IP3 is een berekend punt (de blauwe lijn buigt af).In dit punt zijn beide LF signalen exact gelijk. Overbrengen naar de vertikale "Y" as geeft het fameuze IP3.
Wat vertelt ons dit allemaal ? De groene lijn "minimal discernable signal" horizontaal vertelt ons dat de ruis daar zo groot is EN alle signalen kleiner dan dit niveau op de antenne niet kan gelezen worden (MDS als afgekort). Tussen dit MDS en compressie punt ziet U de "dynamic range" . Onnodig om nog verder te willen gaan, meer LF zal U niet krijgen.
Wat hoger gezien laat ons twee belangrijke gegevens afleiden:
IP3 = (0,5 IMD) + Pin	Dr = 2/3 ( IP3 - MDS)
IP3 = interceptie punt in dBm IMD = verzwakking van het intermodulatie produkt dB Pin = Vermogen aan de ingang F1, F2 in dBm	Dr = dynamic Range IP3 = interceptie punt in dBm MDS = minimum discernable signal
Het is nog niet gedaan: ruis van de lokale oscillator :
Elke ontvanger maakt gebruik van een lokale oscillator (LO in English). U voelt het aan, hoe zuiverder het spectrum van dit signaal hoe beter. De technologie bepaalt de prestatie van de ontvanger. ...
"Faze ruis" wordt door de methode en constructie van de oscillator bepaald. Om de types van oscillatoren in te delen moeten we een manier hebben om dit uit te kunnen drukken. Faze ruis kan uitgedrukt worden door dBc/Hz , weze in dB in verhouding met de drager per Hz.
Een kristal gebruik zal een goede zuiverheid van signaal kunnen opleveren. Een spectrum analyser kan dit visueel maken (Amplitude in functie van de frequentie). 100 % zuiverheid toont op het scherm één enkele vertikale streep wat ideaal zou zijn.
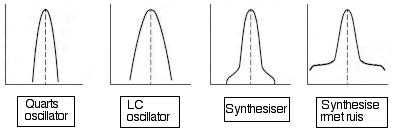De werkelijkheid nu: de kwarts zit er het best uit. De LC ziet er minder fris uit. De syntesiser vertoont hier wat meer breedte maar met minder grote niveau's. Naarmaten de ruis groter wordt ziet U op laatste figuur omheen de gewenste frequentie meer signalen. Hieruit kan men bepalen dat in die mini trancievers of ontvangers, dat men wel moet uitkijken als er synthesisers worden gebruikt. (alles heeft ook nadeel)
De bredere figuren hierboven zal men mogelijks kunnen opmerken op een gewoon oscilloscoop. De sinus vorming van het oscillatie signaal zal wat minder zuiver zijn. Het moet dan wel al stevig verkeerd gaan. Anders uitgedruk:t de werkelijkheid is dat aan een perfect sinus vormig signaal er ruis onder de vorm van faze invloed toegevoegd werd.
Hoe plakken we daar nu cijfers op:
Faze ruis ook wel SSBPN (Single Side Band Phase Noise) genoemd zal gemeten worden enkel aan een zijband van de grondgolf. De manier van werken: er wordt een verhouding gemaakt tussen enerzijds de grondgolf en het resultaat gemeten op een bepaalde afstand maar met een bandbreedte van 1 Hz .
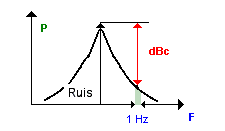Hiernaast een wel zeer onzuiver signaal. We maken één meting van het vermogen van de grondgolf. Daarna maken we een meting op bv 3 kHz van deze een nieuwe meting. Gelukkig zal deze waarde kleiner zijn dan de grondgolf. Deze meting wordt over een bandbreedte van 1 Hz gedaan. (door rekenen wordt een herleiding tot 1 Hz gedaan). We maken de verhouding en drukken in log uit. dat is alles.
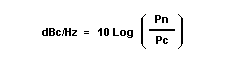In dBc/Hz : dB ten opzichte de drager in Hz Pn : Vermogen op x F afstand van de grondgolf maar over een bandbreedte van 1 Hz. Pc : Vermogen van de grondgolf.
Een voorbeeld :
Op welke manier gaan we deze overdracht van vermogenmeting naar een badbreedte van één Hz doen? Stel , we hebben gemeten over een bandbreedte van 3000 Hz gedaan. We mogen hieruit afleiden dat er 3000 maal minder ruis over een bandbreedte van 1 Hz zal zijn (ruis is gelijkmatig over alle frequenties verdeeld). dit geeft 10Log(3000) = 35 dB minder. Voorbeeld : De uitgang van een oscillator is 0 dBm (1mW), het vermogen van de ruis op 10 kHz van de grongolf is gelijk aan 3 10-9 mW. Rekenen we nu precies uit : 10 Log (Pm/Pc) U zal afgerond -85 dBm vinden.  We gaan nu de herleiding doen naar 1Hz . Hiervoor delen we de gemeten ruis door de bandbreedte of door 3000 we bekomen: 3 10-9 / 3000 = 10-12 mW en verder, 10 Log (10-12  / 1) = -120 dBc/Hz. Impressionant niet ???
En nu, de invloed van de faze ruis op de ontvangst :
Wat er bij ontvangst gebeurt moet toch onze zorg zijn. Wat is de invloed van een slechte oscillator op de eigenschappen van de ontvanger? Bij middel van een voorbeeld wordt dat duidelijk:
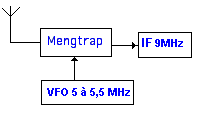Een eenvoudige ontvanger. Een oscillator van 5 tot 5,5 MHz wordt met een signaal op de antenne gemengd (als voorbeeld 14 MHz). De midden frequent is 9 MHz (14 -5 = 9) of de IF (midden frequent). Stel, we ontvangen een station op 14,100 MHz bij een zweving nul. De oscillator staande op 5,100 MHz zal opnieuw een IF van 9 MHz als verschil frequentie leveren. De ontvangst is OK.
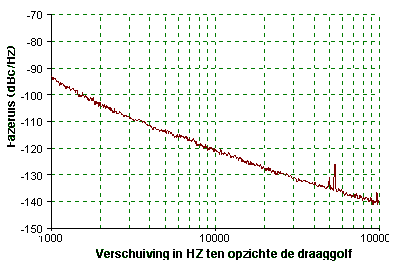U ziet hier de fazeruis van een VFO. We lezen op 10 KHz (10.000) nog een ruis van -120 dBc/Hz. Indien nu een sterk station uitzend op 14,100 MHz zal de ruis op 10 KHz van de VFO zich mengen en het resultaat zal in de doorlaatband van FI (midden frequent) vallen. het resultaat ruis is storend. Deze ruis zal een zekere maskering van het gewenste ontvangst doen. Dit fenomeen wordt ook wel " Reciprocal Mixing" genoemd (wederzijds mengen) . Indien de lokale oscillator luidruchtig is zal dit fenomeen zich frequent voordoen. Natuurlijk, in het andere geval is de ontvanger kalm en rustig.
In Europa, dicht bevolkt, worden we verzopen door sterke stations. Vooral de 14 MHz band laat dit duidelijk horen. In ons voorbeeld hebben we 10 KHz gebruikt. Weet dat dat de helling van een slechte synthesiser geen grote helling vertoont. Hierdoor kunnen storing op vlak van ruis veel sneller voorkomen. Denk er tevens aan dat deze ruisproduktie gevoegd wordt bij de reeds bestaande. Als dan nog zwakke stations doorkomen dan mogen we wel verwonderd zijn.
Tot zover een paar zaken van belang bij ontvangers. Ontmoedigd, nee toch. Voor het examen zal deze stof niet zeer belangrijk zijn maar we wensen toch wel wat meer te kennen dan strikt minimaal. Eens zover zal je in de toekomst in dit hoofdstuk complementaire informatie vinden en in staat worden om met enige kennis een goede van een minder goede ontvanger kunnen onderscheiden. Het stoorstation is niet steeds de stoorder (een indruk die we veelal direct verkeerdelijk opdoen). Kijk in eigen boezem met andere woorden de ontvanger.