De attenuator.

Het is niet altijd versterken dat men in de elektronica moet doen. Vroeger zagen we dat om correct een verbruiker aan een bron te verbinden, het nodig is om de impedantie aangepast te houden. De verzwakker of attenuator zal dan pas correct naar wat verwacht verzwakken, als hier rekening mee wordt gehouden. Dit hoofdstuk zal wat moeilijkheden mee brengen. Immers een paar zaken naar waar we verwijzen werden nog niet gezien. U kan later steeds naar dit hoofdstuk terugkomen.
Inleiding, attenuator of verzwakker :
Atttenuatoren worden meer dan dat U zou denken toegepast. De benaming attenuator of verzwakker laat het al vermoeden: Van een bepaald signaal aan de ingang wordt een deel door de verzwakker opgenomen en omgezet in een of andere vorm van energie (meestal warmte). Aan de uitgang zal men een kleinere spanning terug vinden dan aan de ingang. Het zelfde geldt voor de stroom. Nogmaals, de verzwakker zal dan pas het verwachte gedrag vertonen als men nauwkeurig de elementen van de samenstellen bepaalt. Laten we dit van nabij bekijken. U kan de verzwakker ook zien als een versterker met een negatieve waarde, denk hieraan.
Algemeen gebruik :
Vermindering van het vermogen: U beschikt over 10 W maar Uw transvertor kan maar maximaal 1 W op de ingang verdragen (transvertor is een toestel dat bv een bepaalde frequentiegamma van een zender omzet naar , meestal, een hoger gamma). Zoals U wel weet is een verzwakker van 10 db nodig. Uitbreiding van het dynamisch bereik van een meettoestel: Uw milliWattmeter zal zeker tevreden zijn als aan de klemmen het maximaal toegelaten vermogen niet wordt overschreden. Het dynamisch bereik met 10 laten toenemen doen we dan door eerst een verzwakker van 10 db in de meetkring op te nemen. Calibratie : Door een regelbare verzwakker aan de ingang van een voorversterker te plaats en deze zodanig te regelen dat het zelfde niveau bekomen wordt geeft U de waarde van de gebruikte voorversterker. De attenuator regelbaar in db geeft de waarde van de versterking. Impedantie aanpassing: een verzwakker van 6 db verbetert de aanpassing met 12 db. Deze methode gebruikt men dikwijls bij het aanpassen van een mengtrap door het tussenschakelen van een verzwakking van 50 Ω.
Definitie :
De verzwakker is een opstelling, meestal resistief, die een deel van het beschikbare vermogen zal absorberen. De spelregels van de impedantie moeten gerespecteerd worden.
Met andere woorden kan men deze vergelijken met de spanningsdeler. Ook hier gaat een deel van de energie verloren. Door een oordeelkundige keuze van de samenstellende elementen houdt men de impedantie aanpassingen correct.
We definiëren voor de attenuator volgende karakteristieken :	Zi ingangs impedantie in Ω Z0 uitgangs impedantie in Ω A - verzwakking (onbenoemd) Deze laatste kan men in db uitdrukken wat dan ook meestal het geval zal zijn. De berekening gebeurt als volgt: AdB = 10 Log A
Veel gebruikte vormen :
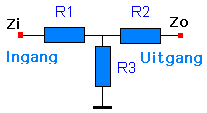
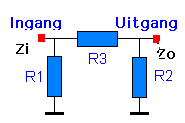
Configuratie in T	Configuratie in π
Zi Z in :ingangs impedantie Zo Z out :uitgangs impedantie A verzwakking, verhouding tussen in en uitgang (onbenoemd)
Berekening van de verzwakking bij T en π:
Meestal zal U de symmetrie tussen weerstanden R1 en R2 opvallen, omdat de vereiste van impedantie aanpassing dit zo stelt. Deze impedanties zijn aan elkaar gelijk. In het overgrote gedeelte van de toepassingen is dat zo.
Let op : Voor de berekening houdt U rekening en respecteer een volgorde van berekenen. Begin met de weerstand R3 en daarna R1 en R2.
Configuratie in T	Configuratie in π
Deze formules laten toe verzwakkers met verschillende in en uitgangs impedanties te berekenen. Het spreekt voor zich dat symmetrische verzwakkers eveneens mogelijk zijn , Zi=Zo.
Berekening van symetrische verzwakker :
Wat hoger vermeld is kan wel omslachtig lijken daarom volgt een uitwerking voor het bijzondere geval dat Zi = Zo zijn , wat meestal voorkomt.
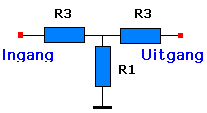
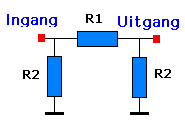
Configuratie in T	Configuratie in π
Z is de karakteristieke impedantie van de verzwakker en n2 is de verhouding Po/Pi, met andere woorden de faktor A in wat vooraf ging. Men moet de vierkamtswortel van Ps/Pe om n als verzwakker te gebruiken.
Wel wat gespecialiseerd maar niet erg ingewikkeld. Let wel op n en n2, en herlees wat hoger beschreven.
Een voorbeeld :
Stel, u wens is een verzwakker van 6 db met een impedantie van 50 Ω te realiseren. We gaan de te gebruiken weerstanden bepalen.	1 - In wat voorafging hebben we gezien dat 6dB in vermogen een verhouding van 4 voorstelt dus:   n2= 4 en    n= 2
2 - Passen we de formules toe voor de symmetrische verzwakker en gebruiken hiervoor de PI (π)verzwakker	4 - 1                   3 R1= 50 ______ =   50   ____  = 37,5 Ω                 2 x 2                   4
Ziehier het resultaat.	2 + 1                      3 R2= 50 _______  =   50    ___  = 150 Ω                 2 - 1                      1
Enkele bemerkingen betreffende het samenstellen van verzwakkers :
Op het eerste gezicht is het bouwen van een verzwakker geen ingewikkelde zaak, en dat is het ook. Maar om ontgoochelingen te vermijden moet men op bepaalde zaken letten....	Op de frequenties waar we de verzwakker zullen gebruiken moeten de weerstanden zich werkelijk als weerstand gedragen en geen reactief element bevatten. Mooie berekeningen geven mooie cijfers maar de beschikbare waarden geven afwijkingen van het gedrag. Temperatuur kan ook gaan spelen. Afin, genoeg, het is niet de bedoeling om te ontmoedigen. Vooral met zorg werken, maar dat doen we toch steeds , of niet ?
Verder: Het vermogen dat de weerstanden moeten verwerken moet oordeelkundig gekozen zijn (temperatuur). Denk er aan dat het deel dat verzwakt onder de vorm van warmte moet worden verwerkt. Tevens is deze dissipatie nodig in het radiofrequent spectrum.	Indien de verzwakker op RF moet werken hebben we meestal coaxkabel verbindingen. Dit om maar te zeggen dat ook de mechanische verwezenlijking uitermaten verzorgd moet zijn. Kies voor dit soort doel , inductiefarme weerstanden.
Een Excel rekenblad voor berekeningen van verzwakkers (later)
Gebruiken van verzwakkers :
We gaan het niet te moeilijk maken en enkel symmetrische verzwakkers gebruiken. (Zi = Zo)	We gaan de karakteristieken van deze verzwakker bij middel van een Ohmmeter bepalen.
	Zie hiernaast onze testverzwakker. De gemerkte waarden van de weerstanden zijn er om de berekeningen te kunnen controleren.
We bepalen de carakteristieke impedantie van de verzwakker :
De te volgen procedure:
	1 - We sluiten de uitgang van de verzwakker kort en meten de totale weerstand aan de ingang zoals de fig aangeeft. Let, we zouden dit ook kunnen berekenen. In alle geval vinden we plus / minus: Ridc = 30 Ω Ridc = ingangsweerstand in DC (gelijkspanning)
	2 - We doen het zelfde maar zonder de aangelegde kortsluiting. Ook hier kan men gaan rekenen als dat de voorkeur heeft. In alle geval is het resultaat: (ook in DC) Rio =  83,5 Ω
Wat nog overblijft is de karakteristieke impedantie bij middel van deze formule te berekenen:
Met volgende resultaat : Zc= wortel ( 30x 83.5) = 50 Ω. Op deze eenvoudige manier kunnen we de karakteristieke impedantie van symetrische verzwakker bepalen.
Reflectie coëfficiënt :
Dit is een nieuwigheid maar zullen hierover meer bij de studie van antennes en feeders zien. Als voorsmaak, zie wat volgt.
Definitie : Dit coëfficient bepaalt de aanpassing van de belasting aan de bron. Ze vertaalt de hoeveelheid van het uitgaande deel van het signaal dat door mis-aanpassing terug naar de bron wordt gestuurd.	De reflectiecoëfficient wordt bepaald als : G (Gamma) of ρ (rho) Indien de aanpassing perfect is is de waarde van G gelijk aan 0 (niks wordt naar de bron teruggestuurd), in het geval van een kortsluiting of een open kring dan is deze waarde G gelijk aan -1 of 1 (alles wordt gereflecteerd)
Passen we deze kennis toe . We houden rekening met de flagrante misaanpassing zijnde kortsluiting of open kring.
We hebben vroeger de karakteristieke impedantie bepaald en berekenen nu: G	Ridc - Zc G = ________          Ridc + Zc
Alle twee de formules zijn geldig.  G = Reflectie coëfficiënt  Ridc = ingangsweerstand in DC  Rio = uitgangsweerstand MET open kring	Rio - Zc G = ________     Rio + Zc
Uit wat vooraf ging kennen we de waarden van de samenstellende weerstanden en hoeven we enkel de formule toe te passen.	30 - 50     -20  G  = ________ =  ___ =  - 0,25           30 + 50     80
Bepalen van  Return Loss  (RL):
Deze notatie komen we vrij frequent tegen in de technische literatuur.	De RL zegt wat over de aanpassing van belasting en de generator en wordt in db uitgedrukt. Men kan dit als een verzwakking door de terugkaatsing zien.
	RL =  10 Log ( G 2 )
In ons geval RL is : 10 Log (0,25 2) = 12 dB
Bepalen van de verzwakking door de verzwakker :
De verzwakking is de helft van RL zijnde AdB =  RL/2 Hier is AdB = 12/2 =  6dB (enkel bruikbaar als Zi en Zo gelijk zijn !).
We bepalen de SWR (tiens voilà ?) :
SWR (Standard Wave Ratio) , een uitdrukking welke we eveneens later nog zullen terug zien, staat voor "staande golf verhouding. Berekenen als volgt :
1 + G SWR =   _______               1 -  G	in deze formule neemt men:       G= ( wortel G 2  )
wat ons in dit voorbeeld geeft :	1 + 0,251 SWR=   ____________   =  1,67              1 - 0,251
We merken hier dat voor een verzwakker van 6 db we nooit een SWR groter dan 1,67 kunnen verkrijgen.
Nota : Weze U er zich van bewust dat wat we tot nu berekend hebben enkel geldig is voor het geval dat in en uitgang gelijk zijn en dat alle weerstanden zich zuiver resistief gedragen. Zoals verwacht is de werkelijkheid anders, vandaar de zorg welke bij eventuele bouw vereist is.
Heel wat nieuwigheden kwamen aan bod en staan in verband met zaken die in deze cursus nog niet werden behandeld. Daarom zal je later terug moeten grijpen naar dit hoofdstuk.