De brug bij wisselspanning
De brug bij wisselspanning
![]()
| U zal zich nog wel de Wheatstone brug opgebouwd uit weerstanden herinneren. Dan weet U nog dat deze brug uit vier armen zoals hieronder getoond is opgebouwd. Uit de kennis van drie van de vier elementen kan men de laatste vrij eenvoudig berekenen. Zelfde principes zullen we gebruiken om een zeer precies meetsysteem op te zetten. |
|
Effe Uw geheugen opfrissen : |
|
|
|
Rechts het bekende schema. Het meettoestel met de "NUL" centraal zal een brug in evenwicht duiden als aan bepaalde conditie is voldaan. Op dat moment zullen de spanningen op beide aansluitpunten exact gelijk zijn. Er vloeit geen stroom door het meettoestel. Een klassiek meettoestel zou ook kunnen maar dan moet U ervoor zorgen dat het steeds volgens de heersende polariteit aangesloten wordt. In sommige gevallen zou dit voor wel bedoelde soort meting waarbij die polariteit op voorhand gekend is kunnen. De nuttige uitslag van de naald is dan groter. U mag gerust deze evenwichtstoestand eens narekenen. :U berekent voor beide delen de spanning over R1 en R2 (een zelfde referentie gebruiken AUB) .... enz |
|
R3
X R1 R2 |
U moet tot de formule rechts komen, en verder: R1. X = R2 . R3 R2. R3 X = _________ envoudig toch ? R1 |
| Met cijfers nu. Zie het schema rechts. We leggen een spanning van 10 V aan. U zal merken dat de brug in evenwicht is. Reken maar na, het is een goede oefening. Uit de formule hierboven kunnen we schrijven:100 x 200 = 500 x 40 een andere manier om de formule te onthouden. |
|
|
Wat met een brug met AC ? |
|
| Deze basis theorie is voor wisselspanning eveneens geldig. AC zullen we eerder voor onderdelen bij wisselstroom gebruikt. Evenwicht van de brug kan maar indien de impendantie en niet meer enkel de weerstandswaarden gelijk zijn. | |
| Brug van Maxwell : |
|
| Mooie naam niet. Deze brug wordt voor het bepalen van onbekende inductanties gebruikt. Ziehier hoe... |
|
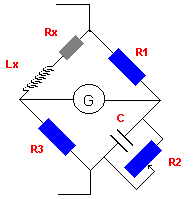
|
Opnieuw de drie delen van de brug maar toch eerst iets anders. Rx, stelt de ohmse weerstand van de spoel voor. Deze is , zoals U weet, steeds aanwezig. We brengen de brug tweemaal in evenwicht namelijk eens voor DC en eens voor AC. Uit volgende formules kan je de onbekende inductantie en eigen weerstand van de spoel bepalen. : |
|
Lx = R1 R3 C Rx = (R1 R3)/R2 |
|
| Brug van Sauty: |
|
| Gebruikt om onbekende capacitanties te bepalen. U ziet twee weerstanden en twee condensatoren waarbij Cx de onbekende is. | |

|
Eveneens een klassieke brug. C1 is een gekende waarde van een stabiele condensator. Met wat rekenwerk komen we er wel uit. Wisselstroom vormt de voeding van de brug. De detectie "G" is niet zomaar een galvanometer maar een systeem met zo weinig mogelijk invloed op de brug. De brug is zoals steeds in evenwicht als de potentialen over "G" identiek zijn. Hieruit leiden we af:I R1 I1 = C1 I2 en R2 I1 = Cx I2 We leiden hieruit af dat R1/R2 = C1/Cx om verder: |
|
C1 R2 |
|
| Brug van Wien : |
|
| Een zeer bekende naam en dus belangrijk. De brug bestaat essentiëel uit een banddoorlaat filter samen gesteld uit een serie en een parallel kring. |
|
|
|
U herkent links toch beide filters? Onze WIEN brug bestaat uit twee RC cellen. Dit is een selectief filter voor een bepaalde frequentie. Deze frequentie is : 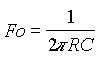 |
|
|
Zoals steeds een vorm zoals de anderen. U herkent een serie en een parallel structuur van weerstand en capaciteit. De symbolen met kleine x zijn de onbekende. Rx is de eigenweerstand van de condensator, waarde in serie. Een wisselspanning vormt de voeding van de brug. De frequentie is hier belangrijk want als deze niet goed gekozen is zullen we nooit de schakeling als bandpas voor die frequentie kunnen gebruiken. Eigenlijk kan U ook omgekeerd werken als de elementen gekend zijn en men de frequentie wenst te bepalen. Dit zijn een paar ideeën waar U kan aan werken |
| Er bestaan nog andere types van brugschakelingen van de zelfde voorloper: de brug van Wheatstone. Alhoewel de moderne technologie steunend veelal op processoren, de brug aan belang wat verminderd is. Voor ons amateurzenders is deze nog voldoende actueel. Een goed gebruik van de brug laat met wat vaardigheid goede metingen allerhand toe. Het moet dus niet verbazen dat we deze ook terug vinden bij metingen aan antennes en/of transmissie lijnen. Hiervan weet U dat het om complexe impedanties gaat in serie (R+/- JX) bij een welbepaalde frequentie. In het kort een inleiding tot deze techniek ... |
|
|
|
|
| Wat schematisch en vereenvoudigd ziet U hierboven een schema van een toestel waarmee complexe impedantie ,onderanderen, in serie kan gemeten worden. De voeding is hier een HF generator, een zender met aangepast niveau, of ruisgenerator. Het onderdeel "G" is nu een HF ontvanger. Eerst zal men met een verbindingsklem de twee rode punten verbinden om daarna de antenne aan te sluiten. De ontvanger helpt bij het aflezen. De instellingen zullen de complexe waarden aanduiden. Zeker, deze uitleg is wat te beperkt maar U vermoed dat de mogelijkheden de moeite waard zijn. Zo een toestel zal naar behoren werken als en de componenten en bouw van prima kwaliteit zijn. Parasitaire "dingen" komen nu eenmaal regelmatig roet in het eten strooien | |
| Tot zover de geschiedenis van de brug. Dit hoofdstuk is informatief voor hen die wat meer dan het strikte minimum wensen te kennen. Het pricipe van het basisschema is wel belangrijk daar dit bij andere gelegenheden nog aan bod zal komen. |
|