Capaciteitsmeter

De capaciteit meter

Als we willen gaan knutselen dat doen we dat met onderdelen die we kennen. Het kan dus nodig zijn om een onderdeel te gaan meten. Een condensator waarvan de waarde niet meer leesbaar is zullen we dan meten. Er bestaan meer dan een soort meettoestel. Sommige "multimeters" zijn hierop voorzien. Het lijkt complex maar dat is het niet. Daarom geven we geen bouwschema mee.


In gespecialiseerde tijdschriften zal U regelmatig wel een schema tegen komen. Zoals steeds hoe complexer hoe groter de mogelijkheden en precisie. Meestal zijn de meetprincipes gebaseerd op de drie volgenden. Alle drie steunen ze op de eigenschappen van de condensator zelf.

1 - Werkwijze met Ohmmeter
Een kleine montage en eenvoudig meetset gaat ons toelaten redelijk precies de waarde van een condensator te bepalen. Het schema hieronder laat één en ander zien. Doorheen de serieschakeling vloeit zoals U wel weet een gemeenschappelijke stroom . Met een eenvoudig multimeter kunnen we de spanning over de verschillende elementen meten. Men noemt deze methode daarom ook "methode met drie voltmeters.
	De spanningen over spoel en condensator staan in quadratuur ten opzichte deze over de weerstand. De frequentie van het signaal uit de generator moet gekend en toch aan de montage aangepast zijn. Voor kleine waarden van C (ook van L) zal de frequentie hoger moeten zijn. Het wordt nu mogelijk met wat rekenwerk ω te bepalen..

De spanning over de condensator is Uc De spanning over de spoel is Ur De spanning van de generator is Ug

We weten toch nog dat Uc = I/Cω en dat I = Ur/R Vervangen van I door de gemeten waarde, en leiden de waarde van Uc af (spanning over C) Ur I= ___ R Ur Uc = _______ C R ω hieruit volgt de waarde van C : Ur C= ___________ Uc R ω

Op papier oogt dit mooi maar de werkelijkheid is wat omslachtig (goed en correct met een rekentoestel omgaan helpt). Eerlijk gezegd, deze methode is wat zwaar.



2 - Methode via de resonantie :
	We vormen zoals hierboven of hiernaast met de onderdelen een serieresonantie kring. De condensator is ONGEKEND. Er moet nog een veranderlijk element gebruikt worden om dit voorbeeld tot resonantie te brengen. We kunnen dit via de generator doen maar ook via een regelbare spoel. De eerste methode zal wel gemakkelijker zijn. In elk geval zoeken we de resonantie om daarna de waarde van C te bepalen. L MOET gekend zijn. Volgende formule zal U niet onbekend zijn:
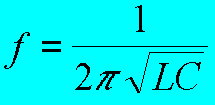	Indien nodig blader terug in deze cursus. De formule van de resonantie ziet U links en de afleiding om C te berekenen hieronder. 1 C = ________ f² 4 π ² L

De twee tot hier aangehaalde methodes zijn moeilijk in bouwschema om in een doosje te plaatsen realiseerbaar.



3 - De brug van Sauty :
	U herkent zeker de klassieke brug maar wat aangepast. Twee weerstanden werden door condensatoren vervangen. Een ervan is onze onbekende condensator Cx. Een generator voedt dit systeem. Een AC spanning dus. Zoals met elke brug kan men via G zien wanneer de brug in evenwicht is. Ongeacht de frequentie kan evenwicht bekomen worden door in te werken op, ofwel R1, R2 als C1. De waarden moeten in elk geval afleesbaar zijn. We brengen de brug in evenwicht en werken verder uit. Het spreekt voor zich dat ook hier "G" (de generator) hoog impedancie is. Belasten van een meetobject induceert steeds fouten.
R1 I1 = C1 I2 en R2 I1 = Cx I2 Hieruit halen we R1/R2 = C1/Cx	Wat ons brengt tot : C1 R2 Cx= _______ R1
U hebt gelijk als U zegt dat dit niet vlot in een doosje ingebouwd kan worden. Er moet dan ook een andere maar betere methode bestaan...



4 - De methode via de lading van de condensator :
Uit de studie van de condensator en gelijkstroom weten we dat een condensator een bepaalde tijd vraagt om opgeladen te worden. De tijd hangt af van de weerstand doorheen de welke de laadstroom vloeit maar ook de waarde van de condensator. Des te groter de weerstand des te groter de tijd is om op te laden. Immers de laadstroom wordt kleiner. De lading van een condensator is afhankelijk van zijn waarde en de stoom voor de lading.	Als we erin slagen de tijd voor volledige lading te meten dan hebben we gewonnen.

De formule hier rechts toont dit verband tussen de samenstellende elementen. V of de aangelegde DC spanning kennen we of kiezen we. E meten we. Voor R nemen we een gekende waarde en de rest volgt:	V = E ( 1 - e^{^{- t/RC}}))
Deze formiule geeft de spanning over de condensator in functie van de tijd op voorwaarde dat de weerstand correct gekend is.	U (haha) zorgt er voor dat we "t" kennen en we bepalen de condensator. Rekenen maar. Bedenk eens effe: we nemen nog steeds aan dat een condensator na 5 tijdconstanten ( RC) geladen is. Deze tijd zal wel gemakkelijker te bepalen zijn. Dus aan U om verder in te vullen.

Weeral niet praktich om in een doosje te stoppen. Het gaat meer om "bricollage" en dit is ook waardevol. Beschik je over de centen, er bestaan toestellen in een doos.