de SWR, VSWR, en gevolgen

Staandegolven, SWR, VSWR

Men kan zijn uiterste best doen bij de bouw, plaatsing van antennes, de voeding en zo meer, maar hoe kan men dat controleren of een en ander correct zijn verlopen. Er bestaan inderdaad toestelletjes die het ons duidelijk kunnen maken. Wat is de bedoeling van meten. We gaan de (voltage) standing wave ratio VSWR of standing wave ratio SWR bepalen en hieruit lessen trekken.
Er volgt nu een vereenvoudigde uitleg.

Definitie :

De SWR, VSWR (staande golven) volgen uit de verhouding als gevolg meetbaarheden van een niet correct aanpassen van bron, voedingslijn en antenne.

Interpretatie :

Energie vertrekt van bv uw zender en vloeit naar de antenne waarvan we hopen dat maximale uitstraling gebeurt. Door het niet perfect zijn zal een al dan niet groter deel van de energie terug naar de bron gestuurd (gerefelecteerd) worden.

Des te meer de afwijking van perfect aanpassen gebeurt des te meer er terug gekaatst zal worden.

De tekening hiernaast kan wat helpen. De blauwe lijn laat het verloop van de energie (spanning) zien wanneer er perfect aangepast gewerkt wordt. In het andere geval gaat er een terugkaatsen gebeuren. Grootheden (spanning en stroom) zullen steeds uit beide delen (heen en terug) samenstellen of opgeteld worden. Langs de lijn heerst er een niet meer constant verloop (rode lijn).
U merk duidelijk staande golven, een beetje zoals bij het aanslaan van een gespannen touw welke men doet trillen (ga effe terug in Uw memorie naar dat spelletje)

Des te groter de bubbels des te groter zijn de staande golven. We gaan nu pogen het waarom duidelijk te maken

Wat gebeurt er bij de belasting (antenne of andere verbruiker) ?

De belasting kan zijn :

Zuiver weerstand wat in het geval van een in ressonatie zijnde antenne het geval is (afgestemde kring). De impedantie wordt dan : Z=R
Zuiver weerstand MET een capacitieve componente. Een antenne welke wat korter is dan deze bij resonantie. PM: de werkfrequentie is RF. De impedantie wordt nu : Z = R - jCw
Zuivere weerstand met een element van inductantie. Een weinig te lange antenne voor de gebruikte frequentie. De impedantie wordt nur : Z = R + jLw

Bij mis aanpassing zal U staande golven ontmoeten. Vereenvoudigd: een "feeder" met een impedantie verschillend aan deze van de verbruiker (antenne) is de kwaal.

Zijn staande golven genant ?

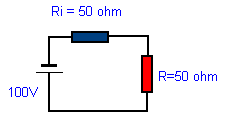
Dit is relatief. In veel gevallen als deze toestand niet te fel van het ideale afwijkt is eerder het negatief gevoel dat de gebruiker ondervindt groter dan het werkelijk effect.
Staande golven veroorzaken enige bijkomende verliezen van energie in de voedings lijn. Op zich zullen staande golven geen interferentie bij andere gebruikers veroorzaken (TV). Immer U moet er rekening mee houden dat er minder energie wordt uitgestraald. Een misaanpassing kan wel Uw eind versterker aardig belasten of zelfs doen sneuvelen. Als het waren ziet die versterker een andere belasting dan de inwendige impedantie van zichzelf. De teruggekeerde golven zien op hun beurt een belasting (die inwendige weerstand van de eindtrap) en deze zal gaan dissiperen. In dit laatste zit het grootste gevaar.

We gaan trachten met een voorbeeld zoals hieronder met DC spanning wat duidelijkheid te brengen.
We gaan de drie mogelijke gevallen eens gaan be-cijferen. De generator met eigen weerstand van 50 Ω een voedingslijn van eveneens 50 Ω maar verschillend belast. 25, 50, 75 Ω. We bepalen voor de drie gevallen het verbruik in de belasting :

I= U/R I= 100/ 50+25 = 1,33 A

Het verbruik door R :

P = RI²

P = 25 x 1,33² = 44 W

I= U/R I= 100/ 50+50 = 1 A

Het verbruik doorr R :

P = RI²

P = 50 x 1² = 50 W

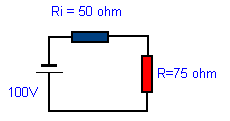I= U/R I= 100/ 50+75 = 0,8 A

Het verbruik door R :

P = RI²

P = 75 x 0,8² =48,6 W

Er gebeurt GEEN optimale overdracht van energie, dat is duidelijk, indien de waarde van de belasting niet 50 Ω bedraagt.
Het is hier dat de staande golven ons plezier gaan bedreven. We gaan hier verder en dieper in en zullen zien dat dit fenomeen pas genant wordt bij grote waarde van terugkaatsing.

We gaan verder met deze studie met DC :

Basis gedachte :

We doen hier de studie met DC spanning niet voor niks. Om de verdere uitleg te kunnen volgen is wat werbeeldings kracht en voorstellings vermogen nodig.
VSWR zien we in verband met RF. Toch bekijken we de zaak vanuit DC standpunt.Een doordenker: als we RF bekijken over een uitermaten klein tijdsinterval (vb pico sec) dan kunnen we toch stellen dat we met DC van uitermaten korte duur te maken hebben.
Bij het aanstuiten kijken we naar de bron , de feeder en op zeer grote afstand (relatief ) de belasting. Deze staat op orde van grote golflengten.
De bron ziet op dat moment een lijn met karakteristieke impedantie als belasting. (de eigenlijke belasting is dan nog niet merkbaar. Na verloop van tijd zal dit DC blokje de belasting bereiken en dan verandert de zaak.
We zullen verder dit verhaal afmaken onder twee voorwaarden, juiste en verkeerde aanpassing.
Als een belasting met Z1 via een transmissie lijn Z2 maar verschillend, dan ontstaat weerkaatsing van een deel van de energie in de tegengestelde richting. Afhankelijk van de faze op dat moment onstaan staande golven veroorzaakt door het aftrekken of optellen van de teruggekeerde golf aan de invallende golf.

We proberen dit verder te analyseren.

Correcte aanpassing

Mis aanpassing

Kijk naar volgende opstelling :

Uw voorstellingsvermogen is van belang.
Een gelijkspannings generator met intern een weerstand 50 Ω voedt via een 50 Ω lijn een belasting van 50 Ω.

Kijk naar volgende opstelling :
Een gelijkspannings generator met intern een weerstand 50 Ω voedt via een 50 Ω lijn een belasting van 75 Ω.

Op de belasting (verbruiker) = 50 V, de stroom is 1A en de spanning over de klemmen: R = 50V
Het opgestuurde vermogen wordt zonder bijkomend fenomeen verbruikt (geen terug sturen van energie)

De stroom is nu 0,8 A en de spanning over de klemmen van: R = 60V.
Nu gebeurt er iets raar. 60 V waar komt die vandaan, want van de bron is maar 50 V vertrokken.
Op het moment van aankomst op de belasting wordt het schema anders. Voor die aankomst hadden we enkel : de bron met als belasting de karakteristieke weerstand van de feeder.
10 V wordt terug naar de bron gestuurd om een correcte toestand te behouden.
Over de lijn staat nu 40 V.
Een zelfde redenering kan men met stromen doen. Plots verandert de stroom (1 A) naar 0,8 A. Hoogst merkwaardig.

Reken maar na....

Met RF zal de terug gestuurde golf zich met de invallende combineren. De zaak wordt complex maar weet dat :

Men rekening met de eigen verzwakking van de feeder moet houden.
Door het combineren de impedantie langsheen de feeder continu verandert.
Dat het zou kunnen voorkomen dat als het gereflecteerd signaal opnieuw bij de bron komt dit volledig verdwenen kan zijn door het eigen verbruik van de feeder. Zelfs bij TOTALE misaanpassing zou dit kunnen voorkomen.
Besluit: Als de feeder een eigen verbruik heeft dat aanzienlijk is en de lengte van de feeder voldoende lang en zelfs zonder belasting er toch niks aan het begin van de lijn wordt gemeten. HET LIJKT ER OP DAT DE AANPASSING JUIST IS.!!! Wel een mooie antenne lijkt mij....

Het voorbeeld hier gegeven is enkel een illustratie van het verhaal.
We zullen het verder zien: staande golven zijn een gevolg van een misaanpassing tussen de voedingslijn en de belasting (of ook tussen belasting en feeder of beide) gezien over de volledige lengte van de lijn. De impedantie verandert steeds zodat stroom en spanning van waarden veranderen. Dit gebeurt volgens een cyclus van kwart golven.(1/4 l).

Definities :

SWR of VSWR (Voltage Standing Wave Ratio).
We kijken nu naar verschillende manieren om dit uit te drukken.

Dit is de manier zoals reeds gezien. Omdat VSWR steeds groter dan de eenheid is moet men deze uitdrukking nemen die ermee overeenkomt. De grootste waarde bovenaan de verhouding. (de teller dus)

Vi Staat voor de aankomende spanning en Vr voor de weerkaatste.

Belangrijk: wat U aan de bron zou meet is niet wat er aan de belasting gebeurt, vergeet dat niet. In een omgeving (frequentie en lengte van de feeder) met weinig of bijna geen verlies zal U dat niet merken.

Reflectie coëfficient :

De reflectie coëfficient ρ is gelijk aan:
Steeds het grootste getal boven de breukstreep.

Reflectie coëficient is niet het zelfde als staande golf verhouding !!

V weerkaatst
ρ = ____________
V invallend

Wat rekenwerk levert ons:
Verwar R weerkaatst en invallend niet met Vmax en Vmin

SWR - 1
ρ = ____________
SWR + 1

Wat verder rekenen en we bekomen de formule rechts.

1 + r
VSWR = _______
1 - r

VSWR met een reactieve belasting :

We gaan werken met een genormaliseerde impedantie van 50 Ω voor de transmissie lijn.De belasting zelf kunnen we als volgt voorstellen ( Zc = r+/- Jx ) dus in serie, en in ons geval bekende waarden.

We normaliseren nu naar 50 Ω

De belasting is een serie schakeling van
Zc = r +/- j x

We normaliseren
        r                         x
R = ___     et X = ____
       50                       50

VSWR heeft de waarde van :

Neem deze formule maar aan.

Reflectie coëfficiënt anders :

Vroeger nogal eens uitgedrukt in percent:

Vter
Ref coëf = 100 _____
Vinv

VSWR bepaling vanaf de twee vermogens.

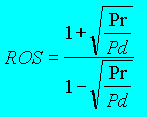Links de formule en neem deze ook voor waar. De voorwaarde tot gebruik is de mogelijkheid om beide vermogens goed te kunnen meten.
Pr = Terug gekaatst vermogen in W
Pd = Invallend vermogen in W

Le return loss :

Een andere manier om de misaanpassing en gevolg te benaderen is de notie "return loss" of verleis door reflectie.

De RL uitgedrukt in dB stelt de verhouding invallend en gereflecteerd vermogen voor. Anders uitgedrukt het niet door de belasting opgenomen vermogen door de mis aanpassing.

Een voorbeeld: stel Uw zender levert ter hoogte van de antenne 100W . Het niet uitgestraald vermogen bedraagt 25W. We berekenen RL

RL = 10 Log 100/25

RL = 6 dB

Met de curve hierboven kan U Rl aflezen.

= SWR

Uitgaande van RL, Kan men de VSWR bepalen door van de formule links gebruik te maken.

Hier boven een vrij eenvoudig te gebruiken grafiek om de VSWR te bepalen.

Verlies bij misaanpassing :

Verlies door misaanpassing (ML -mismatch loss) kan U als je er zin in hebt met de formule links gaan bepalen.

Voor de onspanning, bereken een voorbeeld van Ml voor een toestand waar een VSWR van 3 of reflectie coëfficient van 0,5 werden gemeten.

ML = 10 Log ( 1- 0,5²)
ML = 1,25 dB
Voor de hogere frequenties is de invloed groter en sneller nefast.

We beschikken wel allemaal over rekentoestelletjes maar de tabel hieronder maakt een en ander eenvoudiger toch. :

SWR	RL in dB	r	P geabsorbeerd door de belasting in %	Pgereflecteerd inn %
1		0	100	0
1,1	26,4	0,05	99,8	0,2
1,2	20,8	0,09	99,2	0,8
1,3	17,7	0,13	98,3	1,7
1,4	15,6	0,17	97,2	2,8
1,5	14	0,2	96	4
1,6	12,7	0,23	94,7	5,3
1,7	11,7	0,26	93,3	6,7
1,8	10,9	0,29	91,8	8,2
1,9	10,2	0,31	90,4	9,6
2	9,5	0,33	88,9	11,1
2,5	7,4	0,43	81,6	18,4
3	6	0,5	75	25
3,5	5,5	0,56	69,1	30,9
4	4,4	0,6	64	36
5	3,5	0,67	55,6	44,4
6	2,9	0,71	49	51
7	2,5	0,75	43,7	56,2
8	2,2	0,78	39,5	60,5

We zijn er ons van bewust, de stof werd redelijk diepgaand behandeld. Kan dit Uw honger naar meer opwekken, zoveel te beter. Indien U er in slaagd het mechanisme wat duidelijker te zien dan zijn we op de goede weg. We onthouden:

SWR of VSWR onstaat door misaanpassing.
Rechtstreeks meten kan met speciaal toestel.
Als U beide vermogens kan meten kunnen alle effecten bij middel van grafiek en/of tabellen bepaald worden.
Een grote SWR hoeft niet altijd strikt negatief te zijn.
Verlies arme feeder beïnvloed slechts in kleine maten.
Alleen en denkt daar aan, Uw eindtrap moet er tegen kunnen. Moderne toestellen zijn hierop berekend en zullen automatisch het vermogen uit gaan beperken.

Terug naar RCL Home page.

Bewerking : ON4AWN, Herman Van Meerbeeck