Lijnen deel 2 - ON4AWN

Les lignes -Lijnen deel twee

Kennis over VSWR is en blijft een belangrijk onderwerp. Daarom is het nodig gebleken om deze stof over twee delen te brengen. We gaan hier redelijk diep op de materie in en het dient gezegd, U hoeft deze stof voor het examen niet grondig te kennen. U wordt aangeraden om het programma BIPT hierover te raadplegen.

Fysische en elektrische lengte van een voedingskabel :

Er werd reeds over gesproken, er bestaat een verschil tussen fysische en elektrische lengte van voedingskabel afhankelijk van de "velocity factor". Naar maken deze de eenheid benadert hoe minder de invloed word. Men benadert de snelheid van het licht in het luchtledig of gewone lucht.

Er zijn meerdere redenen om deze fysische lengte van de voedingslijn te kennen. Voor de handliggend, de te verwachte verliezen van de voedingslijn is er één. Het is mogelijk om de werkelijke impedantie nabij de zender te bepalen (begin van de voedingslijn). Deze laatste informatie is belangrijk want voor Uw zender is het DEZE impedantie die elektrisch van belang is.

fysische lengte
elektrische lengte= _________________
verkortingsfactor

Lf
De = _____
v

De lengte van de lijn kunnen we ook in functie van golflengten uitdrukken. Het volstaat de elektrische lengte te delen door de golflengte

Le
n λ = ____
λ

En tot slot kunnen we de lengte van de lijn (fysisch) uitdrukken in fracties van ° 360 graden en de golflengte. U weet toch nog dat om 1 cyclus van het Rf te doorlopen dat de bron 360 graden als het waren doorloopt (het gaat hier over wisselstroom - ga even terug naar dit hoofdstuk als het nodig is). De vector daar ter spraken draait 360 ° om een cyclus te doen.

Le x 360
L° = ___________
λ

Bij middel van een simulatie gaan we de elektrische lengte van een lijn van 20 m lengte en een verkortingsfactor van 0,66 voor de verschillende frequentie banden onderzoeken.

V = 0,66 L = 20m	Freq band	80m	40m	20m	15m	10m	L fys Le = _____ v
	Elektrische lengte	30,3m	30,3m	30,3m	30,3m	30,3m
	aantal λ	0,35	0,7	1,41	2,12	2,83
	Elektrische lengte uitgedrukt in °	127°	254°	150°	44°	298°

Verlies op de weerkaatsing :

Ken Uw tegenstrever. Verliezen trachten we steeds te vermijden. Zijn deze geen onbekende meer dan kunnen we er beter mee omgaan.
Hoofdzakelijk vonden we deze op drie domeinen terug. Voor een stuk kennen we al een deel.

Ohmse verliezen wat wie vermogen zegt sprrekt ook van stromen. Stromen veroorzaken vermogenverlies. Elk type kabel heeft er wel. De verliezen zijn recht evenredig met de lengte van de kabel. De kwaliteit staat omgekeerd met de verliezen.
Het "skin effect". Naarmate de frequentie stijgt zal de stroom meer naar de buiten zijde van de geleider gaan vloeien. Niet moeilijk te begrijpen dat hierdoor de weerstand zal groter worden daar het nuttige oppervlak kleiner wordt.
Diëlektrische verliezen. De isolatie van een kabel is eveneens niet het ideaal. Elk isolator vertegenwoordigt toch een zekere weerstand. Het dient gezegt dat deze zeer groot is maar toch niet onbeduidend. Bij stijgende frequentie zal dit soort verlies gaan groter vorden. Als we een equivalent schema maken van een geleider dat wordt de weerstand die het nverlies vertegenwoordigd paralel over de geleider.
Verliezen door de aanwezigheid van SWR. Door het effect van weerkaatsing zien we aanzienlijk grotere stromen en spanningen langs de lijn ontstaan. Het vermogen dat alzo verloren gaat zal groter worden bij stijgende SWR. Als de SWR gelijk aan 1 is (ideale aanpassing) dan zijn de verliezen minimaal.

Een poging tot het becijferen van de verliezen :

We kunnen twee gevallen onderscheiden :

- Decametrisch, en we zullen dat verder zien, zijn de verliezen zeer weinig van tel.

- bij VHF en hoger ligt het probleem anders. Bij ontvangst ligt de ruis aanzienlijk hoger (het gaat niet om uitwendige ruis als atmosferische en andere). Indien nodig herlees het betreffende hoofdstuk.

Signaal verlies bij Uw correspondent als gevolg van vermogensverlies bij uitzending.

Informatie van W4RNL - L.B Cebik

lt22.gif (6568 octets)

Niks om er nachtmerries van te krijgen niet? Kijk toch maar goed want er moet al langs zend kant 75 % vermogenverlies optreden om bij ontvangst over 1 "één" "S" punt op te merken.

Om het nog duidelijker te stellen (hopelijk) Bestudeer onderstaand grafiek. Volgens de waarde van SWR (inkleuren weergegeven) ziet U in functie van de frequentie het verlies in een kabel van type RG213/KX4 De VSWR evolueert van 1,1 tot 5,1 of een "plage" van 5.

Opnieuw, het beeld komt van W4RNL - L.B Cebik

lt23.gif (8691 octets)

Welke besluiten kunnen we hieruit halen ?

Dat op de lagere frequenties zelfs met een aanzienlijke SWR de verzwakking zelf aan de lage kant is. Op de hogere frequenties tot zelfs een SWR van 5 we toch maar een stijging van 2db van het verlies merken... U zal met reden opmerken dat de invloed van VSWR niet mag overdreven worden.
Vergeet toch maar niet dat het hier over decametrische banden gaat. U zal om de reden hier beschreven Uw DX niet aan Uw neus voorbij zien gaan (toch niet om deze reden).!!

We bekijken nu het voorbeeld van de tweedraads geleider "bifilair of twin" :

Banden :		3,5	7	10	14	18	21	24	28
coax	ros=1	0,35	0,5	0,7	0,75	0,8	1	1,1	1,2
bifilaire	ros=1	0,1	0,11	0,12	0,15	0,16	0,17	0,19	0,2
coax	ros=5	0,75	1,2	1,4	1,7	1,9	2,1	2,2	2,5
bifilaire	ros=5	0,25	0,3	0,35	0,4	0,42	0,45	0,47	0,5

U ziet dat twin beter scoort dan coax. Verlies toch maar niet uit het oog dat het gebruik delicater is dan coax.

Equivalent schema van een transmissielijn :

lt24.gif (2353 octets)

U merkt de shunt weerstand "G" (parallel) die de diëlektrische verliezen voorstelt en weerstand "R" de ohms verliezen 'eigen, scin effect'.
Rechts ziet U de formule die U toelaat de impedantie van de lijn te berekenen.

lt25.gif (1231 octets)

We gaan nu kijken wat er in een lijn van 50 Ω gebeurt in het geval er verschillende belastingen worden aangesloten. :

Zoals U weet is dat het geval met de meeste antennes indien deze hoog genoeg boven de begane grond staan. De hoogte moet U ziet met betrekking met de golflengte. Dit is meestal niet goed mogelijk. Men merkt dat in dat geval de reactie van de aarde niet te verwaarlozen is. Uw antenne accuraat geknipt volgens de golflengte zal van de ideale impedantie afwijken.

Bij het louter knippen op de door U uitgerekende lengte zal het niet mogelijk maken om de SWR beneden een aanvaardbaar peil te brengen. Hoe kan dat nu....??

Een school voorbeeld: U beschikt over een lengte X een kabel van 50 Ω . Dank zij een speciaal toestel kunnen we de impedantei van de antenne bepalen en deze is 150 Ω. De antenne is zuiver resistief. Dit laat toe te stellen dat:

Z = 150 +j0

Een SWR van 3 in ons systeem is het gevolg. Deze waarde is aanvaardbaar. De VSWR of SWR is constant over de ganse lengte. We merken wel over een lengte van een halve golf dat niks constant is en dat elke halve golf we het zelfde observeren.

Volgens W4RNL - L.B Cebik zien we figuur hier onder:

lt26.gif (11636 octets)

In het groen : de reactantie
In rood : de weerstand

Op de X as, staat de lengte in halve golf maar uitgedrukt in graden.

Besluiten :

de SWR is gelijk aan 3 en constantl.
De weerstandswaarde en reactantie veranderen steeds.
De reactantie is capacitief van 0 tot 90° om inductief te worden van 90 tot 180°
Natuurlijk is er vanaf dat er een reactantie meespeel er een faze verschuiving tussen stroom en spanning.

Het resultaat is een steeds veranderende impedantie. Dit is het gevolg van het feit dat de belasting verschillend in impedantie is met deze van de voedingslijn. De SWR is constant en gelijk aan 3. Meetbaar is dit moeilijk want met gewone toestellen zullen we steeds fout meten.
De verschillen in weerstand en reactantie (ook fase) die we langs de lijn terug vinden zijn een gevolg van de staande golven. We lezen een paar waarden op de grafiek af. Op 20 ° worden de weerstand en de reanctantie genuld en op 160 ° is de weerstand 15 Ω en reactantie 70 Ω . Stroom en spanningen zullen dus steeds verschillend zijn.

Fel vereenvoudigd volgt nog een korte uitleg:

Een diagramma door ingenieur Philipp Smith uitgevonden is voor de (zeer) gevorderde van groot nut.Het gebruik zou ons veel te ver gaan leiden op dit niveau van cursus. We beogen een kennis making en meer niet.

lt27.gif (6923 octets)

Zeer in het kort. De horizontale as vertegenwoordigd d de weerstand. De deels cirkelvormige lijnen staan voor reactanties (positief voor inductief en natuurlijk negatief voor capacitief).

Er werd naar 50 Ω genormaliseerd. Dus 50 Ω is gelijk aan 1.0 . een geoefend gebruiker kan heel wat gegevens uit dit instrument halen. Maar het weze genoeg op dit niveau.

Berekening van SWR als de karakteristieke impedantie van de lijn en belasting gekend zijn :

Als U die gegevens kent kan U de SWR van de lijn bepalen.

Rl= weerstand van de belasting
Xl =reactantie van de belasting
Zo= impedantie van de lijn

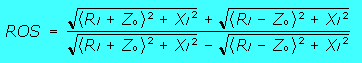We zijn wel ver gegaan met dit hoofdstuk. Bepaal zelf tot waar U de studie wil doen. Grondige studie zal menig avond vullend zijn maar ook aangeraden.

Terug naar RCL Home page.

Bewerking : ON4AWN, Herman Van Meerbeeck