Een volgende schakelmogelijkheid is parallelschakeling. We zullen dit noteren met het teken "//".

Werkwijze :

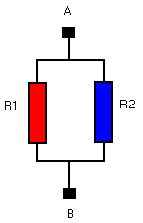
Schakelen we een weerstand van 10 kΩ en één van 20 kΩ in parallel (zie het schema hiernaast): wat is de waarde van de vervangingsweerstand ?

Misschien is het niet duidelijk, maar deze waarde is lager dan elk van de samenstellende weerstanden !

Wat is hiervan de verklaring ?

De stroom uit punt A zal zich verdelen over de beide weerstanden. Nadien vloeien beide stromen terug samen naar B. Er is geen enkele reden dat de stroom in A verschillend zou zijn dan in B. Bedenk tevens dat de spanning die men zou aanleggen over A en B voor beide weerstanden identiek is. Anders uitgedrukt I = I1 + I2

Vereenvoudigde benadering voor de // schakeling:

Wat verder uitgediept :

De totale stroom is gelijk aan de som der deelstromen

Omdat het om breuken gaat, is de uitwerking wat moeilijker maar toch duidelijk.

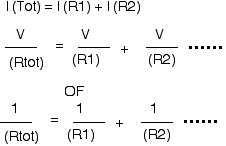
In het bijzonder geval van twee weerstanden:

1            1xR2   +    1xR1              R2 + R1
---  =      -------------------- =       ------------
Rt                 R1   x  R2                R1 x R2

Verder uitgewerkt geeft dat :

Rt =        R1  X  R2
               R1   +  R2

Met andere woorden: de totale weerstand is de verhouding van het produkt op de som ( enkel voor twee weerstanden ). Bij meer dan twee weerstanden kan je ze twee per twee nemen en zo uitwerken.

Is dit wat te moeilijk, geen nood hier volgt een voorbeeld:

R1 = 50  Ω
R2 = 100 Ω
R3 = 200 Ω                 Wat is het resultaat ?   ( We weten al dat het resultaat kleiner dan 50 Ω zal zijn)

1            1       +     1    +     1
--   =    ----          ----        -----    herleiden tot gemeenschappelijke noemer:
Rt          50            100       200


1                  1 x 100 x 200       +         1 x 50  x   200          +          1 x 50 x 100
--- =           ----------------                   ------------------                   -----------------
Rt                  50 x 100 x 200                50 x 100 x 200                     50 x 100 x 200


1              20000     +   10000    +    5000                        35 000                35
---  =        ------------------------------------       =          -------------   =      -----
Rt                       1 000 000                                         1 000 000             1000


Om Rt te kennen keren we de breuk om :

Rt = 1000/35   = 28,57  Ω   

Wat commentaar :

1 - het is wat langer en moeilijker om te doen.

2 - de kans op een fout is wat groter.

3 - het resultaat MOET in elk geval kleiner zijn dan gelijk welke van de // geschakelde weerstanden.

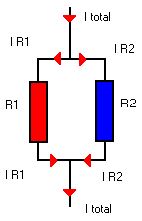
Nog niet gedaan ... wat met de stroom ?

Eigenlijk hebben we dat al gezien, maar dit is belangrijk genoeg om herhalen:

                   U                                 U
   I_R1   =   -------                I_R2   =  --------
                   R1                               R2

Tot besluit nog een praktijkvoorbeeld

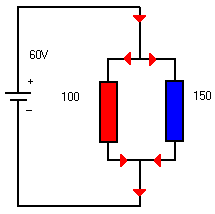
Nemen we een spanningsbron V van 60 V die twee weerstanden in // voedt.
R1 = 100 Ω
R2 = 150 Ω
Hoe groot is de stroom doorheen elke weerstand en welke waarde van stroom wordt uit de bron betrokken ?

We kunnen ofwel de stroom in elke weerstand bepalen en de som maken, ofwel de vervangingsweerstand berekenen en bepalen welke stroom de bron door deze stuurt. Werken we volgens methode 1.
           U                  60
IR1 =  ---   =         ------   =   0,6 A
           R1                100


           U                  60
IR2 =  ---   =         ------   =   0,4 A
           R2                150

De totaalstroom = 0,6 + 0,4 = 1 A

Controle van de berekening, maar volgens methode 2 :

         R1 R2            100 x 150           15 000
Rt =   --------  =    ------------     =   --------- = 60 Ω
         R1 + R2         100 + 150            250

                U                60
I total =  -------   =   ------ = 1 A
                Rt               60

Download een rekenblad in Excel