Theorema van Norton
![]()
Theorema van Norton
![]()
Om kringen te kunnen
uitrekenen is dit theorema even belangrijk als dit van
Thevenin. Op zich is deze kennis niet direct onontbeerlijk
voor het examen, maar het kan wel helpen bij de uitwerking
van wat complexere kringen. Aan jou de keuze. Principe
: het volstaat om volgende
principes te begrijpen: We bepalen eerst de weerstand. Deze
is gelijk aan deze uit Thevenin, dus geen probleem.
Vervolgens bepalen we de kortsluitstroom. Hiervoor vervangen
we de belasting door een kortsluiting en bepalen de stroom.
Deze stroom zal de maximum stroom zijn die de bron zal
kunnen leveren. Blijft nog de belasting aan te sluiten en de
stroom doorheen deze belasting te bepalen of te
berekenen. Opgepast: we gebruiken
hiervoor het principe van proportionaliteit zoals bij de
spanningsdeler. Let er op dat het om stromen gaat, met als
gevolg dat we deze verhouding volgens het parallelprincipe
moeten toepassen (de stroom splitst zich in twee delen )
Gelijkaardig
als de studie van het theorema van
Thevenin.![]()
Thevenin reduceerde de complexe kring tot een
spanningbron in serie met één
weerstand. Parallel hierop werd dan een belasting
aangesloten. De werkwijze van Norton is gelijkaardig maar we
gebruiken de omzetting via een stroombron en een
parallelweerstand.
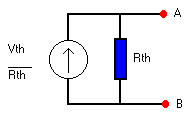 Eigenlijk
niet echt moeilijk...
Eigenlijk
niet echt moeilijk...
Hoe gaan we te
werk ?
Eerst voor de weerstand
van Norton: Deze is identiek aan
Thevenin, daarom passen we dat strikt toe (ook in de
berekening), enkel met dit verschil dat deze weerstand in
parallel op de stroombron komt (anders loopt er geen
stroom). Vervolgens de
stroom: We sluiten de belasting
kort ( in het echte schema ) en berekenen de stroom die dan
zal vloeien.
deze waarde is : ![]()
Verander de kring volgens
Thevenin in een kring volgens Norton:
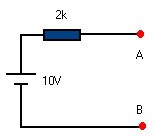
Hiernaast zien we een
kring volgens Thevenin. We weten dat de weerstand identiek
maar parallel op de belasting staat bij de vervanging naar
stroombron (zie beide schema's links).
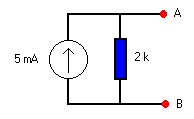
We bepalen dan de stroombron: we sluiten punten A en B kort
en bepalen de stroom die dan vloeit.
Vth
10
I = _____
I= _____
= 5 mA
Rth
2000
Merk het resultaat hiernaast.
Een voorbeeld zal één en ander hopelijk verduidelijken
Bekijk het schema
hiernaast:,
Bereken de stroom in RL als RL = 1 - 2 et 8
kΩ worden
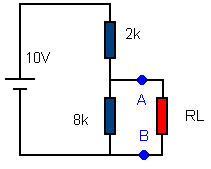
Bereken de weerstand van
Thevenin : 1 - Maak de belasting
los.
2 - Sluit de spanningsbron kort en bepaal de weerstand.
Merk 2k//8k = 1600 Ω
Bereken de kortsluit
stroom : 1 - Vervang de belasting
door een kortsluiting.
( een goede raad: teken bij elke stap het schema
)
De 8 kΩ
wordt kortgesloten, blijft enkel de weerstand van 2000
Ω
in de kring.
Icc = 10/2000 I cc= 5 mA
Volgend schema is het
resultaat van deze redenering :
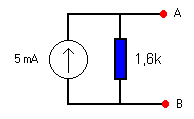
Sluit de weerstand van
1000 Ω aan
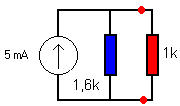
Passen we het principe van
de proportionaliteit toe (cfr. de spanningsdeler, maar nu
met stroom) We hebben nu een stroom
van 5 mA die splitst in twee ongelijke stromen Rth en
RL.
Merk op dat in de weerstand met de kleinste waarde de
grootste stroom zal vloeien.
De stroom doorheen RL :
IRL = ![]() =
= ![]() = 3,08 mA
= 3,08 mA
Op gelijkaardige manier Rth :
![]()
Blijft nog het rekenwerk
voor de andere waarden van belastingen.
Aanrader: probeer het zelfde maar nu door gebruik te maken
van het theorema van Thevenin.