Wisselstroom: de transformator
|
De transformator is een zeer belangrijk onderdeel in veel schakelingen. "Transfo's" worden niet alleen in voedingen gebruikt maar ook frequent in de radio-elektronica waar ze de overdracht van energie verzorgen door magnetische koppeling. |
|
|
Het principe : |
|
|
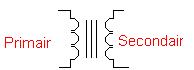
De transformator bestaat uit twee wikkelingen die onafhankelijk zijn: een primaire en een secundaire wikkeling, beide gewikkeld op een gemeenschappelijke kern ( die kern kan bestaan uit een magnetisch materiaal of lucht ). |
 |
|
Waarvoor dient een transformator ? |
|
|
Een transformator is een erg belangrijk onderdeel voor veel schakelingen. Transfo's worden niet enkel in voedingen gebruikt, maar ook vaak in de radio-elektronica waar ze de overdracht van energie verzorgen door magnetische koppeling. |
|
|
Werkingsprincipe : |
|
|
De primaire wikkeling wordt door een sinus-wisselstroom doorlopen ( ook andere golfvormen zijn mogelijk ). De kring is dus gesloten. De wikkeling kan voorgesteld worden als een inductantie L met reactantie X waardoor een stroom I loopt. De stroom I veroorzaakt een veranderende flux volgens de wisselfrequentie en de golfvorm. De veranderende flux vloeit doorheen de magnetische kring. Aangezien de magnetische kring ook geldt voor de secundaire kring of wikkeling, wordt deze spoel door een veranderend magnetisch veld doorlopen. We hebben al gezien dat in een spoel die zich in een veranderend magnetisch veld bevindt, een elektro-motorische kracht ( EMK ) wordt opgewekt. Bijgevolg is aan de klemmen van de secondaire wikkeling, een wisselspanning te vinden overeenkomstig de parameters van de transfo. |
 |
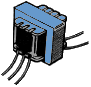 |
Links een mogelijk voorbeeld van een veel gebruikte voedingstransfo. |
|
Regels of conventies : |
|
|
De fysische grootheden van de primaire worden door de index 1 aangeduid.
|
De fysiche grootheden van de secondaire worden door de index 2 aangeduid.
|
|
Samenstelling of opbouw : |
|
|
De magnetische kern is een gesloten kern. Bij een voedingstransfo bestaat de kern uit magnetische ijzerplaatjes, het éne boven het andere en in vorm geponst. Het gebruik van plaatjes van weekijzer vermindert de Foucault stromen ( Dit zijn stromen die verliezen in de kern veroorzaken ). |
De wikkelingen bestaan uit geïsoleerd koperdraad. We vinden minstens twee wikkelingen ( méér kan ook ), met elk hun eigenschappen). Eén is de primaire en de andere is de secundaire wikkeling. Beide wikkelingen ( of meer ) zijn meestal elektrisch van elkaar geïsoleerd. |
|
Transformatieverhouding : |
|
|
We hebben al vermeld
dat bij een transformator de secundaire spanning, hoger, lager of gelijk kan zijn dan de primaire spanning. Er bestaat dus een vast verband tussen de
primaire en secundaire wikkeling. Men noemt dit de
transformatieverhouding
aangeduid als "m". |
|
|
U2 N2 m = ____ = ____ U1 N1 |
|
|
Hoe luidt dit verhaal voor stromen ? |
|
|
Laten we dit praktisch
bekijken. Onze transfo is verondersteld verliesvrij te zijn. Daardoor zal
de energie die we er in stoppen aan de primaire, ook gelijk zijn aan
deze door de primaire geleverd. : P1= P2. |
|
|
I2
1 |
I1 |
|
We herhalen dat de stroomverhouding overeenkomt met het omgekeerde van de transformatieverhouding. |
|
|
We zouden kunnen zeggen dat de de transformator enkel dient om spanning of stroom te "verhogen" of te "verminderen". Een concrete toepassing: bij een audioversterker wordt er naar gestreefd om maximaal energie naar de luidsprekers te sturen. We hebben al gezien dat de maximale energieoverdracht gebeurt als de bron en de verbruiker dezelfde eigen weerstand vertonen. Een voorbeeld: de audioversterker heeft een belastingsweerstand van 200 Ohm. De luidspreker die men wenst aan te sluiten heeft daarentegen een zeer lage eigen weerstand van 4 Ohm. Dit is een ongunstige toestand: beide moeten met elkaar in overeenstemming gebracht worden. We moeten, met andere woorden, de impedanties op elkaar aanpassen dat kunnen we precies doen met een transformator. |
|
|
Aanpassen van impedanties |
|
|
We stellen Z1 als de
impedantie van de primaire en Z2 als de impedantie van de
secondaire voor. |
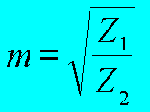 |
|
Dit is een formule die we even onthouden . Rekenen we nu het voorbeeld van hierboven uit ( de aanpassing 200 Ohm naar 4 Ohm) uit. Welke verhouding in de transfo moeten we kiezen ? m = vierkantswortel (200/4) = 7 Met andere woorden: de secundaire moet 7 maal minder wikkelingen hebben dan de primaire. Onze transfo levert een kleinere spanning bij een grotere stroom, wat duidelijk verwijst naar een zelfde vermogen. |
|
|
Terug met de voeten op aarde, naar de werkelijke wereld : |
|
|
Tot nu toe hebben we aangenomen de er bij de transformatie geen verliezen optreden. Niets is minder waar. Kleinere transfo's, zelfs bij nullast ( zonder belasting ) gaan opwarmen van zodra er een spanning wordt aangelegd. Vooral Foucaultstromen zijn de oorzaak (verliezen in de magnetische kern). Ook de weerstand van de wikkelingen is een bron van warmteverliezen. Deze Foucaultstromen zowel als de opwarming door eigen draadweerstand stijgen met de nominale stroom. Dit verlies doet de werkelijke secundaire spanning dalen zodat op de secundaire een kleinere spanning verschijnt dan theoretisch verwacht. Nog andere verliezen zoals strooivelden of verlies aan flux buiten de magneetkern verminderen de goede werking, met als gevolg een verlies aan rendement van de transformator. Naargelang de kwaliteit van de transfo beter is, zal het volume groter zijn ( dikkere draden, betere kern, afscherming ...) en het prijskaartje hoger. Het rendement kan je berekenen door de verhouding te bepalen tussen secundair en primair vermogen en dit eventueel met 100 te vermenigvuldigen om het in % uit te drukken. |
|
|
De auto-transformator : |
||||||||||
|
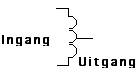
Een bijzonder type transformator zie je hiernaast. Merk op dat de secundaire en primaire wikkelingen NIET MEER gescheiden zijn. Als je uitgaat van het aantal wikkelingen dan stel je vast dat, zoals hier getekend, de secundaire spanning steeds kleiner is dan de primaire. Als je de transformator omkeert dan is deze verhouding ook omgekeerd. Op vlak van veiligheid is elke klem steeds met het net verbonden. Als je de nul-referentie van je schakeling aanraakt, kan je ook een fase van het elekriciteitsnet aanraken en dat zal je wel voelen !! Het grote voordeel van dit soort transformator is dat er minder koperdraad voor nodig is dan bij een klassieke transfo, wat kostenbesparend is. |
 |
|||||||||
|
Het vermogen bij transformatoren : |
||||||||||
|
Dit wordt altijd in VA (Volt Ampère) uitgedrukt. Bij onze studie werd niet met faseverschuivingen rekening gehouden, maar die zijn er wel degelijk, en zelfs veel. Daarom is het beter om het maximumvermogen dat de transfo kan leveren op deze manier aan te duiden. Op verliezen na, is P1 = P2. Meestal is het rendement van een transformator om en bij de 0,85 - 0,9 of 85 tot 90 %. |
||||||||||
|
Transformatoren op HF : |
||||||||||
|
Je zal ( hopelijk snel !) veelvuldig transfo's in HF-schakelingen gebruiken. Meestal zal het om afgestemde kringen gaan. De energie wordt op dezelfde wijze van primair naar secundair doorgegeven en zo verder naar de versterkertrap(pen). Ring- of toruskernen worden veelvuldig gebruikt. Behalve de prijs bieden ze verschillende voordelen. Veldverliezen worden vermeden omdat de flux in de ringkern geconcentreerd wordt. Bovendien is een ringkerntransformator klein en gemakkelijk te monteren. Zo een kern bestaat uit een ring van ijzerpoeder of ferriet, waaraan men volgens de samenstelling bepaalde eigenschappen kan geven. Ze worden vooral op hogere frequenties toegepast, maar bestaan ook voor lage frequenties. Door middel van een kern kan je de eigenschappen van de spoel beïnvloeden. Als je L verandert, wijzig je op die manier de afstemfrequentie van de LC-kring. In afgestemde kringen of middelfrequentfilters zie je vaak een kern waarmee je de waarde van L en dus ook de frequentie kan bijstellen. Er bestaan kernen uit ferriet maar ook uit aluminium dat tegengestelde eigenschappen vertoont. Een samenvatting wordt in de tabel hieronder gegeven: |
||||||||||
|
||||||||||