Werkwijze om de impedantie van serie- of parallelkringen te berekenen

Nu volgt een wat meer wiskundige uitleg om impedanties te bepalen. Deze aanpak wordt ook wel imaginair of complex rekenen genoemd. Dit hoofdstuk is niet direct belangrijk voor het examen: voor de fijnproevers zou ik zeggen.
Enkele bijzonderheden :
Toen we de impedantie van een seriekring bepaalden, hebben we genoteerd dat deze uitgedrukt wordt als 6,7 Ω met een stroom uit faze van 26,6 °.
Deze notatie wordt ook wel eens polaire coordinaten genoemd. Grafisch kan men dit voorstellen zoals hiernaast: De impedantie kan men ook in de vorm van rechthoekige coördinaten voorstellen: 1 e deel : de waarde van het resistief deel  (6 Ω in ons voorbeeld) 2e deel : de waarde van het reactief deel (+3 Ω in ons voorbeeld)
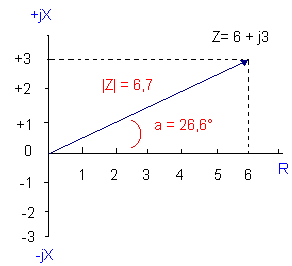
De waarden die we voor een seriekring berekenden, leverden ons een resultaat onder polaire vorm op, m.a.w. Z (impedantie van de kring) is gelijk aan de hypotenusa van de rechthoekige driehoek met als basis de waarde van de weerstand en als hoogte de waarde van de reactantie. Dit systeem is zeker correct, maar het biedt ons een minder duidelijk beeld van de toestand want het geeft geen eenvoudige aanduiding van de aard van de reactantie ( is die capacitief of inductief ?). Dit kunnen we wel berekenen. Het is zo dat dikwijls de rechthoekige coördinaten gebruikt worden.
Enkele details : Een voorbeeld om de impedantie Z aan te duiden:	Z = 6 + j3
Z is de impedantie van de getoonde seriekring, 6 stelt de resistiviteit of weerstandswaarde voor en 3 het reactief deel van de impedantie, alles uitgedrukt in Ohm. Wat nu met die " j " ?	De "j" geeft ons een aanduiding dat we met vectoriële notatie bezig zijn en dat we nooit eenvoudigweg de waarden 6 en 3 mogen optellen. Beide vectoren staan 90 ° op elkaar ( bekijk de tekening). De + staat voor een inductieve reactantie en de - voor een capacitieve reactantie.
De waarden die dit "merkteken" dragen zijn "complexe getallen": we werken dan met complexe impedanties.
Werken met complexe getallen vraagt toch een diepere kennis dan voor het examen nodig is. We zullen daarom wat vereenvoudigen.	Trachten we de polaire waarden via de complexe uit te drukken: Z = 6 + j3 Even Pythagoras toepassen: Z= wortel ( 62 +32 ) Z= wortel ( 36 + 9 ) = wortel van (45) = 6,7 Ω. En kijk, het werkt !
Conventies :
Weerstand  R	Z = R +  j0
Inductie L	Z = 0 +  jLω
Capaciteit C	1 Z = 0   -  j ____                    Cω
Wat uitleg: Eigenlijk niets nieuws. Neem nu een weerstand met de aanduiding van j 0 dan betekent dat, dat er GEEN inductieve reactantie is. De weerstand =0 en de +j voor de reactantie Lw   wijst naar een spanning die voorijlt op de stroom.	Hetzelfde dient gezegd voor de capaciteit. De 0 en de reactantie van de condensator door de -j verwijst naar de spanning die naijlt op de stroom of anders uitgedrukt, de stroom ijlt voor op de spanning.
We stellen vast dat de impedantie voor elk type onderdeel in een kring uit twee delen is samengesteld. Wetende dat: 1 - het reël deel, het resistief deel van de impedantie is. 2 - het imaginaire deel stelt het reactief deel van de impedantie voor. We onthouden:  Z = R + jX of   Z = R - jX
Onze nieuwe kennis toegepast op de basiscomponenten :
We hebben een weerstand van 50 Ω, hoe stellen we dit voor als serieimpedantie ?	Het gaat om een zuivere weerstand dus is het imaginair deel 0. Dan: Z = R en dus Z = 50 + j0
We hebben een condensator van 100 pF, de kring werkt op een frequentie van 50 MHz: wat is zijn notatie ?	Het gaat hier over een reactantie en daarom moeten we met de frequentie rekening houden. We zien dit in de term ω. 1 - Berekening van de reactantie van de condensator C         1                           1 X = ____    =    ________________________        Cω          100 10-12   x 2 x π x 50 106 Dus X = 32 Ω, uitgedrukt als : Z = 0 - j32
We beschikken over een spoel van 10 µH aangesloten op een wisselspanning van 50 MHz, wat is dan de notatie ?	We gaan op een zelfde manier te werk. We weten dat e X = Lω. 1 - berekenen we de reactantie van L X = Lω  =  10 10-6x 2 x π x 50 106 =   3140 Ω dus Z = 0 + j 3140
Om onze kennis nog wat verder uit te diepen: stel we hebben een kring van Z= 48 + j25.
1 - Wat is de impedantie van deze kring ? Eenvoudigweg Pythagoras toepassen en we vinden : Z = wortel ( 482 + 252 ) = 54 Ω 2 - Welk is de fase tussen stroom en spanning en in welke zin ? De zin wordt gegeven door het teken van het reactief deel. In dit geval ijlt de spanning voor op de stroom ( een inductief gedrag). Betreffende de defasering hebben we als tangens = X/R weze 25/48 = 0.52 Om nu de hoek te kennen moeten we ons rekentoestelletje gebruiken ( de ouderwetse rekenlineaal mag ook !) . We zoeken de functie arctangens. en vinden : 27,5	3 - En het complement nu ? om uitdrukkingen te vereenvoudigen. Als voorbeeld Z= 48 +j25. Het complement wordt nu 48 -J25. Voorbeeld : Stel dat we hebben :               1 Y =  __________            48 + j25 Om te vereenvoudigen kunnen we beide termen ( boven en onder ) met het complement vermenigvuldigen. Dit geeft :              48 - j25 Y =   _______________        (48 +j25) (48 -j25)              48- j25            48 - j25 Y =  ___________ =  __________           482 + 252             2929
Werkwijze : Het doel is om op een eenvoudige manier de impedantie en fase in een kring te berekenen, uitgaande van de werkfrequentie en de waarde van de onderdelen. Principe n 1 : We beginnen onze eerste analyse bij de eerste component, de belasting. Vervolgens voegen we de elementen één na één toe richting aansluiting. We voeren een sequentiële analyse uit. Principe n 2 : Wanneer we componenten in // toevoegen, werken we via admittanties (zoals bij // weerstanden). Dit betekent dat EERST die admitantie berekend wordt voor de toevoeging. Principe n 3 : Het omgekeerde van de impedantie is de admittantie genoteerd als Y waarde 1/Z in Siemens Het omgekeerde van de weerstand is de conductantie genoteerd als G waarde 1/R in Siemens Het omgekeerde van de reactantie is de susceptantie genoteerd als B waarde 1/X in Siemens Principe n 4 : Om van Z naar Y of van Y naar Z over te stappen gaan we systematisch de formules toepassen wetende dat de complexe impedantie van de vorm Z= R +jX of Z = R - jX
Startend van Z = R +jX	R                                X Y = _________          - j  _______             R2 + X2                     R2 + X2
Startend van Y = G + jB	G                                B Z = _________          - j  _______             G2 + B2                     G2 + B2
Samenvatting van deze methode:
Overgang van impedantie naar admittantie De uitdrukkingen Berekening van Z voor R  (1) Z =   R  +   j0 C   (2)                     j Z =  0    -  ____                   Cω L   (3) Z =   0   +   jLω Overgang van impedantie naar admittantie van Z naar Y (4)          R                   X Y = ______     - j  _____       R2 + X2           R2 + X2 Overgang van admittance naar impedantie van Y naar Z (5)          G                  B Z = ______      - j _____       G2 + B2           G2 + B2 Werkwijze 1 Plaats de 1e component ( de belasting ) en bereken zijn impedantie Z1= R1 + jX1 door de formules (1-2-3) 2 Voeg de 2e component toe Bereken zijn impedantie Z2= R2 + jX2 door de formules (1-2-3) 3 Vraag : in serie plaatsen? in // plaatsen ? Voeg impedanties bij impedanties, weerstanden bij weerstanden, reactieve elementen bij reactieve elementen. Zt = Z1 + Z2 = Rt + jXt met Rt= R1+R2 en Xt = X1 + X2 Bereken Y1 door formule (4) Bereken Y2 door formule (4) Voeg de admitanties bij admitanties, conductanties bij conductanties en susceptanties bij susceptanties. Yt= Y1 + Y2 = G + jB met met Gt= G1+G2 en Bt = B1 + B2 4 Ga terug indien nodig naar impedanties door formule (5) 5 Voeg de tweede component toe en herbegin bij (2)
Door het downloaden van Exel rekenbladen kan je je kennis controleren.
Berekening van reactantie:	Berekening Z naar Y of Y naar Z
Een probleem :	Dit voorbeeld komt uit het boek "The ARRL UHF/Microwave experimenter's manual" dat ik de geïnteresseerden kan aanbevelen.
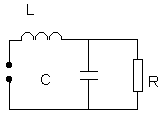L = 1µH R = 50 Ω C = 1 pF f = 1 GHz	We gaan de kring links analyseren en uitrekenen. Gevraagd is de impedantie tussen beide aansluitklemmen en eventueel, de faseverschuiving tussen stroom en spanning. De kring werkt op 1 GHz
	1e stap : Plaats het eerste element, de weerstand. We berekenen zijn complexe impedantie. Dit stelt geen probleem, ze is gelijk aan de definitie: ZR =  50 + j0
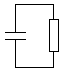	2e stap : Nu plaatsen we het tweede element, de condensator in //.
We berekenen de reactantie van  ( 1/Cω ) de condensator op 1 GHZ: we vinden 159 Ω . Plaatsen we deze waarde in de complexe impedantie  ZC = 0 - j159 Gezien deze twee componenten in // staan bepalen we het resultaat. We moeten daarom via de admittanties gaan. We berekenen vanuit de impedanties, de admittanties van R et C Ter herinnering in het geval van de condensator, (ZC= 0 -j159) is 0 het resistief deel  (R) en 159 het reactieve deel (X)
Voor de weerstand weten we dat: Z = 50 +jo We berekenen nu de twee componenten voor de admittanies, G et B          50 GR = __________ =  0.02 S (Siemens)          502 + 02 en B=0 ( daar j0) we schrijven : YR= 0,02 - j0	Voor de condensator weten we dat: Z = 0  - j159             159 BC = _________     =  0,00629 S             1592 +02 en G = 0 (daar R=0) we schrijven : YC = 0 + j0,00629
Noot : Het zal wel opgevallen zijn dat voor de overgang van impedantie naar admittantie het teken van de reactantie verandert.
Nu kunnen we de admittanties optellen wat ons oplevert: Yt = YR + YC =      (0,02 -j0)  +   (0 + j0,00629)   =   0,02 + j0,00629 We hebben nu de totale admittantie van de kring BC
We gaan nu de impedantie van de kring bepalen. Hiervoor gebruiken we de formule om van Y naar Z te gaan.
Overgang van Y naar Z :                  G                                B Z = _________          - j  _______             G2 + B2                     G2 + B2 wat ons oplevert :                       0,02                                                   0,00629 Z = _________________                - j         __________________             0,022 +0,006292                                   0,022 +0,006292      Dit is de impedantie van de condensator in // in parallel met de weerstand. Z = 45,5  - j14,3
3e stap : We plaatsen de spoel in de kring, dus in serie met de zojuist berekende impedantie.
Ditmaal is de inductantie in serie met de rest. De impedantie kunnen we nu zonder meer bijplaatsen. We berekenen de impedantie van de spoel in serie. Eerst de spoelreactantie Z=Lω Z = 1.10-6 x 2 x π x 1.109 = 6280 Ω We drukken nu de serie impedantie van de spoel uit. We schrijven : Z = 0 + j6283
Nu voegen we de impedantie van de spoel bij de reeds berekende impedantie (zie hoger) : Zt = Z + Zl Zt = (45,5  - j14,3 )  +  (0 +j6283) =      45,5 + j6269 Het is duidelijk dat we nu WEL een algebraische optelling van de weerstanden mogen doen. Dus in dit voorbeeld 45,5 + 0 = 45,5 . Hetzelfde doen we nu voor de reactanties : -14,3 + 6283 = 6269.
Blijft nog het uit fase lopen van de stroom op spanning of omgekeerd. Zoals reeds gezien doen we dit via de verhouding X/R of de waarde van de tangens (of boogtangens). Via de functie arctangens op ons rekentoestel berekenen we de waarde van de hoek tussen stroom en spanning.                        X                  6269 Arctangens  _______  =     ________  =   arctangens (137,8) =  89,6°                         R                  45,5
"Gelukkig" behoort dit niet tot de examenstof. Toch kunnen er geïnteresseerden zijn die na het examen wel wat meer over elektronica willen weten. Dit hoofdstuk vormt een eerste aanzet om ook andere onderwerpen uit te diepen.