Resonantie

In de praktijk zal het, vaker dan gewenst, gebeuren dat een schakeling in resonantie komt. Serie- en parallelkringen hebben een bijzondere eigenschap: zij kunnen onder bepaalde omstandigheden in resonantie komen en gaan trillen. Waar gaat het om ?
Zonder deze belangrijke eigenschappen zou radio-elektriciteit niet bestaan. Een analogie uit de mechanica verduidelijkt dit: we weten allemaal dat het op een brug absoluut uit den boze is om met een grote groep mensen in de pas te marcheren. De brug kan gaan trillen en vernield worden.	Het is de eigen resonantie van de brug die, als ze overeenstemt met het ritme van het stappen, de ineenstorting kan veroorzaken. Onze elektrische kringen kunnen eveneens in elektrische resonantie komen. Indien het bedoeld is kan dat zeer nuttig zijn, bijvoorbeeld in onze ontvangers en zenders.
Laten we dit eens met een praktisch voorbeeld bekijken :
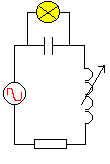	We bouwen de schakeling hiernaast, een klassieke serieschakeling. De spoel is regelbaar. Een lampje wordt over de condensator geplaatst. De totale kring wordt gevoed met wisselstroom.
1 -   We regelen de spoel op het minimum (zowat nul) en sluiten AC ( wisselstroom ) aan op de kring. 2 - We vergroten gradueel de spoel. 3 - en gaan door tot L zowat maximaal is	Er gebeurt niets, de lamp blijft gedoofd of brandt minimaal. Op een bepaald moment zal de lamp fel oplichten. Bij één bepaalde instelling van de spoel vinden we een maximale helderheid. Als we verder draaien gaat de helderheid geleidelijk verminderen en zal de lamp uiteindelijk weer doven.
Verklaring van wat we vaststelden :
Indien we tevens een AC voltmeter over het lampje hadden geplaatst zouden we gezien hebben dat bij maximaal oplichten, de wisselspanning zelfs groter zou zijn dan de aangelegde spanning.
Wat gebeurt er in onze kring ? Als de spoel zowat gelijk aan 0 is, zal de condensator die een bepaalde reactantie bij de aangelegde frequentie heeft, de stroom beperken (idem voor de weerstand). De stroom loopt voor op de spanning. Geleidelijk L vergroten: de reactantie van L gaat van 0 in waarde stijgen.	Op een bepaald moment is de reactantie van L gelijk aan deze van C. Beiden zijn gelijk maar tegengesteld in zin (in tegenfase ) en zullen elkaar opheffen. De totale stroom wordt niet meer beperkt ( afgezien van R ) en is dan in elk geval maximaal. De spoel en condensator hebben elk wel een niet verwaarloosbare reactantie. Dit geeft ons een bijzondere eigenschap als we de spanning over zijn klemmen gaan bepalen : UC =  XI  weze           I UC =  ___         C ω en UL =  Lω I.
We kunnen in een toestand van "overspanning" komen. Deze toestand kan enkel voorkomen indien : XC = XL	Wanneer dit fenomeen zich voordoet, spreken we van de resonantie van deze kring.
Resonantie van een kring RLC of LC in serie of parallel kan enkel voorkomen als beide reactanties aan elkaar gelijk zijn.                                                                   1 M.a.w XL = XC uitgewerkt geeft dit als Lw =    ____                                                                 C   ω
Waarin L en H C in Farad ω = 2 π f f in Hertz
Wat betekent dit nu voor de serie- en parallelkring ?
Basisprincipe : Elke serie- of parallel kring heeft maar één enkele resonantiefrequentie.
Om de zaak niet te ingewikkeld te maken, brengen we de weerstand R niet in rekening ( ideale componenten ). Door de frequentie te laten variëren onderzoeken we het gedrag van de kringen. Met andere woorden, we bekijken de zaak voor frequenties onder EN boven de resonantiefrequentie.
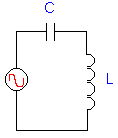
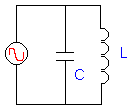
Serie kring	Parallel kring
Voor beide gevallen gebruiken we de zelfde componenten: f = 50 MHz C = 10 pF L = 1µH XL is de reactantie van de spoel. XC is de reactantie van de condensator. Z is de impedantie van de kring . Deze laatste is waar het over gaat. We berekenen de reactantie van de condensator, spoel alsook de impedantie van de kring. Het uit-fase lopen halen we verder uit het gedrag van de kring.
F 10 MHz 50 MHz 90 MHz XL 63 314 565 XC 1592 314 177 Z 1529 0 388   capacitief resistief inductief	F 10 MHz 50 MHz 90 MHz XC 63 314 565 XL 1592 314 177 Z 65 infini 257   Inductief Resisitief Capacitief
In het geval van de serie kring stellen we vast dat bij resonantie de impedantie naar nul neigt (er is geen resitief element). Hieruit volgt dat de stroom maximaal is. Uit de tabel leren we tevens dat onder de resonantiefrequentie de kring duidelijk capacitief is en een stroom voert die voorijlt op de spanning. Immers de reactantie van de condensator is groter dan deze van de spoel. Boven de resonantiefrequentie gebeurt het omgekeerde: de kring gedraagt zich als een spoel.	In het geval van een parallelkring stellen we vast dat bij resonantie de impedantie naar oneindig neigt (er is geen resitief element). Hieruit volgt dat de spanning maximaal is. In de tabel zien we tevens dat onder de resonantiefrequentie de kring duidelijk inductief is en hierdoor een stroom voert die naijlt op de spanning. Immers de reactantie van de spoel is groter dan die van de condensator. Boven de resonantiefrequentie gebeurt natuurlijk het omgekeerde: de kring gedraagt zich als een condensator.
Bestudeer nu bovenstaande grafiek.
Voor de seriekring geeft hij het verloop van de stroom in functie van de frequentie aan.	Voor de parallelkring duidt hij het verloop van de impedantie in functie van de frequentie aan.
Je kan op deze figuur nog wat anders zien. Als we er van uitgaan dat we met een seriekring te maken hebben, geeft de blauwe kleur het verloop van de stroom, maar de weerstand is tweemaal kleiner dan de vorm in violet (tweemaal meer stroom). Hoe kleiner de impedantie bij een seriekring is, hoe groter hij bij een parallelkring is.
Samenvatting voor een serie- en parallel kring.
Bij resonantie Serie kring Parallel kring I maximum minimum U overspanning overstroom (zien we later)   Z minimum maximum
Waar leidt dit ons heen ?
Dit soort kringen gebruiken we bij filters. Om één bepaalde frequentie uit een groot aantal te filteren moeten we over een element beschikken dat de mogelijkheid heeft deze frequentie als het ware te selecteren. Dit kan het geval zijn bij oscillatoren, frequentievermenigvuldiging enz.... Dit soort kringen vormt de basis ven de radio-elektronica.
Verderop gaan we wat dieper op de zaak in met een wat meer wiskundunige benadering.