Vermogen bij wisselstroom
|
Wisselstroom en reactanties ken je al. Vermogen en reactantie zullen wel niet het zelfde als bij gelijkstroom zijn, denk je. Je hebt nog gelijk ook ! |
|||||||||||||||||||||||||||||||||||||
|
Even terug naar gelijkstroom : |
|||||||||||||||||||||||||||||||||||||
|
Nogmaals: bij gebruik van gelijkstroom is het vermogen gelijk aan het product van de spanning en de stroom door de kring. Bij de studie van wisselstroom weten we dat de wet van Ohm ook van toepassing is ALS men gebruik maakt van de EFFECTIEVE waarde van spanning en stroom. |
Maar we weten ook dat de spanning niet noodzakelijk in fase met de stroom is. Bij gebruik van reactanties gebeurt er een verschuiving. We gaan nu zien dat we hierdoor met drie soorten vermogens te maken hebben. |
||||||||||||||||||||||||||||||||||||
|
Vermogen bij wisselstroom : |
|||||||||||||||||||||||||||||||||||||
|
Het schijnbaar vermogen wordt in VA (Volt/Ampere) uitgedrukt. Bij dit soort vermogen komt er geen faseverschuiving aan te pas. |
|
||||||||||||||||||||||||||||||||||||
|
Het reël of actief vermogen of actief, het werkelijke vermogen, uitgedrukt in Watt . Hier komt de vershuiving WEL bij te pas maar volgens de cosinusregel. Stel de verschuiving j. |
|
||||||||||||||||||||||||||||||||||||
|
Het reactief vermogen, Dit zou het verbruikt vermogen door de reactantie zijn als we het inderdaad kunnen verbruiken. Maar een reactieve belasting verbruikt niets zoals we vroeger hebben gezien. We kunnen dit vermogen als VAr(Volt/Ampere reactief) benoemen. |
|
||||||||||||||||||||||||||||||||||||
|
Verband tussen die drie soorten van vermogens: |
|
||||||||||||||||||||||||||||||||||||
|
Vormfaktor k |
De vormfaktor "k" bij wisselstroom is de cos (j) de faze verschuivingshoek spanning / stroom. |
||||||||||||||||||||||||||||||||||||
|
Verband tussen Pa, P et k: |
|||||||||||||||||||||||||||||||||||||
|
Om het actief vermogen te kennen volstaat het om het schijnbaar vermogen en de vormfaktor te kennen. |
P = k . Pa |
||||||||||||||||||||||||||||||||||||
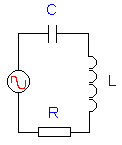 |
Een wisselstroomgenerator levert een spanning van 100 V effectief in de kring. Het vereist wel wat werk maar de tabel
kunnen we nu zelf uitrekenen; belangrijk is de
gevolgtrekking.
|
||||||||||||||||||||||||||||||||||||
|
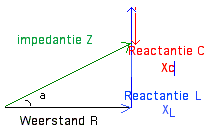
In eerste instantie moeten we de vormfaktor voor het vermogen kennen. Vectoriëel kunnen we de kring als volgt voorstellen: |
 |
||||||||||||||||||||||||||||||||||||
|
Hieruit vinden we de waarde van de tangens, waaruit op zijn beurt de hoek tussen stroom en spanning (arctangens) afgeleid kan worden. |
|
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
Nemen we nu het voorbeeld voor 70 MHz. Het schijnbaar vermogen is 45.8 VA, het actief vermogen is 10.3 W en het rea ctief vermogen is 44.6 VAR. De faze verschuiving is 77
° , en de stroom in de kring is
|
|||||||||||||||||||||||||||||||||||||
|
De elektriciteitsleveranciers hechten bij sommige grote verbruikers veel belang aan cos (j) van het verbruik. Industrieel verbruik is meestal zwaar inductief verbruik ( elektromotoren... ) . Het gevolg is een cos (j) die zeer klein kan zijn. De geleverde spanning is uiteraard vast in waarde. Om een vermogen (U.I cos (j)) te leveren zal het verlies op de voedingslijnen groter worden (RI2). De leverancier zal deze cliënt vragen ( of zacht dwingen ) om deze cos (j) te vergroten om het stroomdebiet daardoor te laten dalen. Dit kan hij doen door voldoende capaciteit, om de verschuiving te nullen of verkleinen, te plaatsen. |
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
Een radioamateur gebruikt meestal het effectief of het actief vermogen. Maar als we reclame over zenders lezen merken we steeds dat een uitgangsvermogen van een zender uitgedrukt wordt onder de vorm van PEP-vermogen (PEP = Peak Envelope Power). |
Waarom vermeldt de fabrikant zoiets ? Wel, het staat mooier in een reclamefolder als men met betere cijfers naar voor kan komen. Wat uitleg: |
||||||||||||||||||||||||||||||||||||
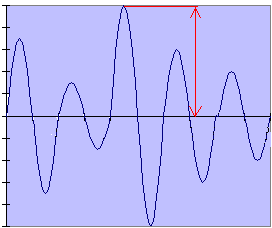 |
Initiëel werd PEP
uitgedacht om het maximum gemoduleerd signaal te kunnen
evalueren. Vermogen, en we denken direct aan Watts dat wil zeggen
het product Ueff en Ieff. |
||||||||||||||||||||||||||||||||||||
|
Het vermogen
Ppep = Um x Im. |
|||||||||||||||||||||||||||||||||||||
|
Het EIRP : |
|||||||||||||||||||||||||||||||||||||
|
Alweer een uitdrukking om zich niet goed bij te voelen, maar nuttig en noodzakelijk. De afkorting EIRP staat voor Equivalent Isotrope Radiated Power. Een antenne straalt in bepaalde richting meer dan in een andere. Ze kan ook "winst" geven. Vergelijken wordt moeilijk. Daarom is het interessant om over een eenvormige vergelijkingsbasis te beschikken: de "isotropische antenne" . Dit is een theoretische antenne die in alle richtingen in de ruimte even veel straalt en zonder enige winst. We zullen hier op terugkomen bij de studie van de antennes. |
|||||||||||||||||||||||||||||||||||||
|
Hoe berekenen we het EIRP ? |
|||||||||||||||||||||||||||||||||||||
|
EIRP is het product van het uitgestraald vermogen en de winst van de gebruikte antenne. |
EIRP = P x G |
||||||||||||||||||||||||||||||||||||
|
Een voorbeeld : Je koopt een antenne waarvan men zegt dat hij een winst vertoont van 6 dbi. Later zullen we zien dat 6db overeenkomt met een verhouding 4 in vermogen. Je zender levert aan de antenne 100 W en voor dit geval beschouwen we de coaxkabel als verliesloos. |
het EIRP zal zijn : |
||||||||||||||||||||||||||||||||||||
|
We zien in een later hoofdstuk nog wat dbW en dbm betekenen. |
|||||||||||||||||||||||||||||||||||||
| Terug naar RCL Home page. |
| Bewerking : ON4AWN, Herman Van Meerbeeck |