De Parallelkring
|
In wat vooraf ging hebben we met een serieschakeling leren omgaan. Parallelkringen zijn wat moeilijker om te bestuderen. Bij de serieschakeling beschouwden we de spanning als wijzigende parameter en de stroom als gemeenschappelijk; nu nemen we de stromen als veranderlijk en de spanning als vast of constant. |
|
|
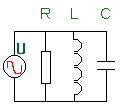
De schakeling : |
|
|
Hiernaast zie je de schakeling. De spoel zou eigenlijk nog een kleine inwendige weerstand moeten bevatten want de ideale spoel moet nog uitgevonden worden. De lekweerstand van de condensator staat uiteraard parallel en kan als vervat in R aanzien worden. Merk meteen op dat de gemeenschappelijke parameter, de spanning is. Deze staat immers parallel op ALLE elementen. |
 |
|
Waarom is de // (parallelschakeling) moeilijker te analyseren dan de seriekring ? |
|
|
Bij de studie van de weerstanden in // moesten we rekening houden met het omgekeerde van de weerstand (breuk). Tegenover weerstand noemt men dit de geleidbaarheid. Hetzelfde gebeurt met reactanties. |
Onthou
dat het omgekeerde van de weerstand ook geleidbaarheid wordt
genoemd. |
|
|
|
|
Bekijken we de figuur rechts : |
|
|
Aangezien de spanning U
gemeenschappelijk is wordt ze als referentie gekozen. De
vectoren vertegenwoordigen de verschillende stromen die door
elk element vloeien. |
|
|
Je kan zelf vaststellen dat er niet veel verschil is met de serieschakkeling. Het is enkel wat moeilijker om in stroom te redeneren. Merk wel: |
IR is in fase met U
(natuurlijk) |
|
Om de totaalstroom te kennen moeten we onvermijdelijk naar de vectoriële optelling van de stromen gaan. |
__
__ __ __ |
|
Bekijken we nu deze vectoren : |
|
|
De wet van Ohm leerde
ons dat I = U/R en anderzijds dat de spoel IL = U/Xl of |
De stroom door de weerstand: I = U/R.
|
|
Wat spelen met I (verplaatsen) en we krijgen : |
I2 =
U2 /R2 + (
U/Lω
- UCω)2 |
|
Tot zover deze studie. |
|
| Terug naar RCL Home page. |
| Bewerking : ON4AWN, Herman Van Meerbeeck |