Resonantiefrequentie en kwaliteitsfactor

Uit het vorige hoofdstuk weten we wat resonantie is en hoe we dat moeten begrijpen bij serie- en parallelkringen. We hebben geen kwantificering gedaan. Bovendien hebben we voor de eenvoud maar de beperkingen van de componenten ( onder de vorm van weerstanden ) buiten beschouwing gelaten. Hier komen we terug naar de werkelijke wereld met zijn onvolkomenheden. In dit hoofdstuk gaan we er wat dieper op in en definiëren we ook de kwaliteitsfactor Q.
Bij gelijkstroom was het eenvoudig: een weerstand is een weerstand en alsdusdanig te herkennen. Bij wisselstroom ligt dat wel anders. Je ziet immers niet altijd waar de weerstand zijn invloed laat gelden. Bijvoorbeeld een spoel: die heeft een eigen weerstand: een condensator heeft ook altijd een zekere lekweerstand ( hoe klein ook ) die bovendien nog frequentieafhankelijk kan zijn. Tevens kunnen aansluitdraden zich als spoel of capaciteit gedragen, vooral op hogere frequenties. Tussen de wikkelingen van de spoel bestaat ook een kleine capaciteit. Je merkt het al, er zijn genoeg redenen om NIET perfect te zijn ( de componenten toch ). Voor ons heeft dit als gevolg dat de zaken er niet eenvoudiger op worden. Ook nog op te merken: het skin- effect speelt een grotere rol bij hogere frequenties. Door dit effect zullen de elektronen bij hogere frequenties steeds meer aan de buitenkant van de geleider gaan vloeien. Het gevolg is dat de effectieve doorsnede van de geleider steeds kleiner wordt voor hogere frequenties. Door bijzondere geleiders met zeer kleine eigen weerstand te gebruiken kan men dit effect enigzins beperken ( vandaar het gebruik van zilverdraad of zelfs van vergulde geleiders).
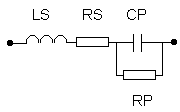
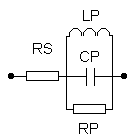
Een reële condensator	Een reële spoel.
Naarmate de frequentie groter wordt, gaat de parasitaire spoel meer invloed uitoefenen en zelfs de reactantie van de echte condensator overtreffen. We hebben dan geen condensator meer maar een spoel! LS is vooral een gevolg van de aansluitdraden. Bovendien kunnen LS en CP bij een bepaalde frequentie in resonantie treden en hiervoor een kortsluiting vormen (op RS na). Rp is de lekweerstand van de condensator	CP is de parasitaire condensator gevormd tussen de wikkelingen van de spoel ( de over de spoel verdeelde capaciteit ) . Rs is natuurlijk de serieweerstand (skineffect !!) verdeeld over de spoel. Ook hier merken we een mogelijke parallelkring op .
Voortaan vervangen we alle parasitaire weerstanden door één enkele waarmee we in het vervolg rekening zullen houden.
We hernemen de seriekring :
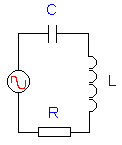	Hiernaast hebben we de klassieke serieschakeling. We laten de generator in frequentie variëren van 5 tot 85 MHz. Telkens berekenen we de reactantie van de condensator en de spoel. Daardoor kunnen we de impedantie van de kring te bepalen. Z en U zijn dan bekende gegevens waarmee we de stroom I en de spanningen over L en C bepalen.
Waarden van de elementen van de kring : L= 1 µH C = 10 pF R = 50 Ω f = instelbaar van 5 tot 85 MHz U = 100 V
MHz 5 20 50.3 70 85 XL 31 126 316 440 534 XC 3183 796 316 227 187 Z 3152 671 50 218 350 I (A) 0.0317 0.149 2 0.458 0.285	Met het rekenblad in Exel kunnen we alle resultaten vinden. Met deze waarden berekenen we de spanningen over R, L en C door eenvoudig de wet van Ohm toe te passen: U= ZI, U= Xc.I en U= Xl.I
MHz 5 20 50.3 70 85 UL 0.98 18.8 632 201.5 152.2 Uc 100.9 118.6 632 104 53.3 UR 1.858 7.45 100 22.9 14.25	We stellen vast dat de resonantiefrequentie op 50.3 MHz staat en dit als XL = XC is, maar dat wisten we al (de wat donkerdere kolom ). Maar: we merken een zeer hoge spanning over L en C en de nominale bronspanning over R. Wat betekent dit ?
De spanning over L en C wordt als het ware vermenigvuldigd met een parameter (spanningsgenerator maal die factor). Deze spanning bij resonantie over L en C bedraagt 632 V. De generator voedt de kring met een spanning van 100 V. We berekenen de verhouding en vinden: Aanloog vinden we hetzelfde resultaat als we de verhouding van reactantie spoel (of condensator) en impedantie Z maken: We hebben hier die vermenigvuldigingsfactor gevonden. Deze factor geldt enkel bij resonantie. We kennen deze beter onder de naam "kwaliteitsfactor" Q van de kring.
Berekenen van Q voor een serie schakeling	XL Q =    ____            R
	met Xl en R en Ω Q is een waarde zonder eenheid of onbenoemd.
Berekenen van Q voor een parallel schakeling	R Q =    ____           X
Merk het omgekeerde bij de elementen in beide formules: zowel de ene als de andere kan gebruikt worden.
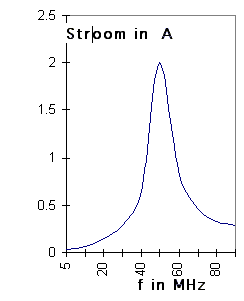	De stroom volgt de curve zoals in figuur hier links. We weten dat de stroom toch beperkt wordt door parasitaire elementen die in serie met de kring verschijnen ( ook R ). In ons voorbeeld kunnen we 50 Ω toekennen wat een stroom van 2 A oplevert bij resonantie ( 100 van de generator en 50 Ω ). Als nu die weerstand bv. 25 Ω bedragen dan is het duidelijk dat de zaak anders ligt.
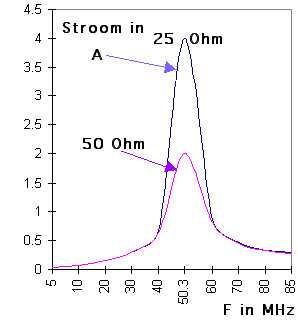	Bekijk de curve voor 25 Ω. We stellen vast dat : 1 - de stroom groter is ( het dubbele ) en dat hij de verhouding van de weerstanden volgt; 2- de helling van de curve steiler verloopt ( violet staat voor 50 Ohm ).
Dit leidt ons naar iets nieuws, namelijk de doorlaatband.
Definitie :
De uitdrukking laat het al vermoeden: een deel van de frequentieband links en rechts van de resonantiefrequentie wordt met kleine verzwakking doorgelaten. Buiten die band wordt ALLES met minstens 3 db verzwakt.	Over de Bel en deciBel (db) zullen we later meer zien; het volstaat om nu te onthouden dat 3db wil zeggen dat de amplidude met 3/10 vermindert.
	Beelden vertellen meer:
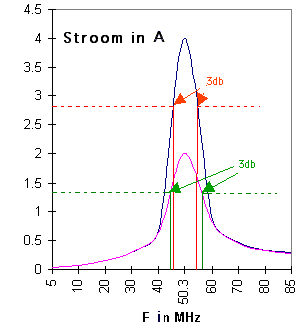	We herkennen de curve zoals bij de serieresonantie op 50 MHz. In het blauw, de curve met Q gelijk aan 12.64 In het violet, de curve met Q gelijk aan 6.32. Op beide curven werden de 3db punten aangegeven aan beide zijden van het resonantiepunt. Dit resonantiepunt is precies in het midden tussen die beide 3db punten gelegen. De kring met de grootste Q-waarde heeft de kleinste bandbreedte, anders uitgedrukt, is de meest selectieve van beide. Hoe groter de selectiviteit des te beter een frequentie of band uit een brede band kan "gefilterd worden". Deze selectiviteit wordt vaak nagestreefd in de radio-elektronica.
We kunnen ook noteren dat de bandbreedte gelijk is aan het quotient van de centrale afstemfrequentie of resonantie, en de kwaliteitsfactor.	f0 B =   __________                Q
	Met B in MHz F0 in MHz Q eenheidloze waarde
Deze eigenschappen worden in veel schakelingen toegepast. Het kan gaan om een grote selectiviteit, waarvoor de kringen met een grote "Q" moeten hebben, of omgekeerd, om een grote doorlaatband wat dan een kleinere "Q" vereist.
Tot nu hebben we de resonantie gemeten, maar ze kan ook berekend worden:
Resonantie zagen we, is deze frequentie waarbij bij zowel serie- als parallelschakeling, de reactanties elkaar uitnullen of opheffen. Anders gezegd: er bestaat geen reactantie meer doordat beide (van C en L) tegengesteld van zin zijn.	In wiskundige termen uitgedrukt :                1 Lω   =    ____               Cω
We herleiden de uitdrukking tot:	LC ω2   = 1
Wetende dat ω = 2 π f helpt ons verder :   LC 4 π2 f 2 = 1       of nog                 1 f 2 =   ___________           LC 4 π2 Blijft de vierkantswortel om f op res te bepalen:
Deze formule is meestal bekend onder de naam "formule van THOMSON". Zoals te verwachten zien we dat de frequentie uitsluitend door L en C worden bepaald. De R is er immers uit verdwenen.
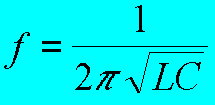Voor sommigen een wat meer praktische wijze om de formule te onthouden.
De formule hierboven is misschien niet zo gemakkelijk om uit te rekenen. Het omgekeerde van de wortel uit ???. We merken ook een constante in de formule nl: 1/2 Ω . Deze uitdrukking kan voor sommigen gemakkelijker zijn. Belangrijk: denk er om dat het uitdrukken van C in bijv. microFarad enz., wel orde in de cijfers vereist. De wetenschappelijke notatie moet steeds correct gehouden worden omdat anders al snel fouten van een factor tien en meer ontstaan.	C L f 2  =  25330
We hebben nu een zeer belangrijk hoofdstuk gezien. Je moet dit absoluut goed kennen en de formule onthouden, of beter nog, de formule kunnen reconstrueren. Leer ook je rekentoestelletje zonder fouten te bedienen ( wie rekent er nog manueel ?).