|
In dit hoofdstuk
behandelen we de condensator als essentieel element in
schakelingen. We beperken ons tot het gedrag en gebruik
bij gelijkstroom; wisselstroom komt later wel aan
bod.
|
|
|
Starten
we met het symbool en een paar voorbeelden :

|
|
|
Opbouw of
samenstelling van de condensator
|
|
Een condensator is
samengesteld uit twee door een isolator gescheiden
geleiders of platen. Het symbool verwijst daar duidelijk
naar.
|
|
Fundamentele eigenschappen
|
|
Een condensator kan
geen gelijkstroom doorlaten ( zie het symbool ).
Wisselstroom kan er onder bepaalde voorwaarden wel
doorgaan, wat we later zullen zien.
|
Men zegt dat een
condensator energie opslaat. Bij aansluiten aan een
gelijkstroom zullen doorheen de isolator, ladingen op de
twee elementen elkaar aantrekken. Losmaken van de voeding
belet de ladingen zich te verplaatsen: ze blijven daarom
op de platen. Het gevolg is dus een spanning of lading
die achterblijft.
|
|
|
|
|
Wat betekent
capaciteit van een condensator ?
|
|
Een condensator kan een
lading opslaan. Deze lading hangt af van:
- de grootte van de
condensator.
- de spanning aangelegd
om te laden.
|
Q = C x V
of

Waarin :
C in Farad
Q in Coulomb
U in Volt
|
|
De capaciteit van
een condensator wordt in Farad uitgedrukt. Maar
één Farad is een te grote eenheid of
waarde. Men maakt van ondereenheden gebruik, zie
hiernaast:
|
Ondereenheden
van Farad
|
|
Farad
= 1
MilliFarad = 10-3 F
MicroFarad = 10-6 F
NanoFarad = 10-9 F
PicoFarad = 10-12 F
|
1 F
1 mF
1 µF
1 nF
1 pF
|
|
Waarvan
hangt de capaciteit van een condensator af
?
|
|
- evenredig met
oppervlakte S van de platen.
- omgekeerd evenredig
met de afstand e tussen de platen of de dikte van het
diëlectricum. (isolatie)
- evenredig met de
diëlectrische constante "er",
dit is een factor
volgens het gebruikte soort diëlectricum.
er voor enkele
materialen:
|
mica
|
6 - 8
|
|
glas
|
4 - 7
|
|
polystreen
|
2,3 - 2,4
|
|
steatiet
|
4,4
|
|
lucht
|
1
|
|
er
S
C =
__________
e
met:
C in Farad
e in meter
S in m2
er
= afhankelijk van het gebruikt
materiaal.
|
|
|
|
|
|
|
|
|
|
Over naar
wat praktijk :
|
|
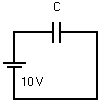
Bekijk het schema
hiernaast:
De condensator wordt
ogenblikkelijk opgeladen. Niets remt de stroom af ( geen
weerstand ).
|
|
|
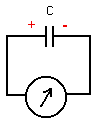
We nemen de bron weg en
vervangen ze door een Voltmeter ( ideaal: geen
belasting):
|
|
|
Dezelfde spanning als
de bron zelf wordt gemeten, hoewel de bron niet meer
aanwezig is.
|
Experimenteel hebben we
kunnen vaststellen dat in de condensator elektriciteit
wordt "gestockeerd".
Positieve lading links
en negatieve rechts op de platen.
|
|
Eenmaal geladen doet de
condensator op zich geen stroom vloeien.
|
Indien het
diëlectricum perfect is, (oneindig grote weerstand)
kunnen de ladingen NIET afvloeien. Men kan het ook zo
zien: de condensator gedraagt zich als een open
schakelaar in een gelijkspanningskring.
|
|
|
|
|
|
|
|
Samenvoegen
van condensatoren zoals weerstanden
|
|
|
|
|
|
|
|
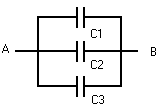
Condensatoren
in parallel
|
Condensatoren
in serie
|
|
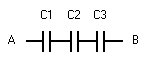
|
|
Door condensatoren
parallel te plaatsen doet men eigenlijk het zelfde als
het vergroten van het oppervlak van de platen. Daarom
moet men dus de waarde van de condensatoren optellen om
het resultaat van de parallelschakeling te
zien.
Dus optellen
!
|
Omgekeerd merkt men dat
hier het totale diëlectricum dikker wordt. Uit de
formule hierboven weten we dan dat de capaciteit kleiner
moet zijn dan die van de samenstellende
condensatoren.
|
|
Het resultaat van de
parallelschakeling van condensatoren tussen A-B
wordt:
Ctotaal
= C1 + C2 + C3
|
Het resultaat van de
serieschakeling van condensatoren tussen A-B wordt:
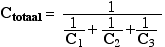
In geval van
geval van twee condensatoren:
 of
of 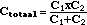
|
|
|
|
|
|
Hopelijk werkt volgend
rekentoestel:
Opgelet: Behoud de
eenheidsmaat om fouten te vermijden (geen µF met pF
mengen, herleid ze tot een zelfde eenheid voor de
bewerking )
|
|
Voer
de waarde van C1 et C2
in
aanpassing van
eenheidsmaat
(indien nodig)
|
|
|
Capa
in //
|
=
|
|
|
|
Capa in Serie
|
=
|
|
|
|
|
|
|
|
|
|
|
Berekeningsprincipe
:
Parallel
geschakelde condensatoren dienen berekend als waren het
serieweerstanden.
Serie geschakelde condensatoren dienen berekend als waren
het parallelweerstanden.
|
|
|
|
Wat gebeurt
er met de energie ?
Energie wordt opgeslagen, dat weten we reeds. Maar
hoeveel, is wat anders.
Voor
het examen hoef je dit niet te
kennen.
|
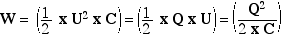
|
|
|
W in Joule
C in Farad
Q in Coulomb
U in Volt
|
|
Elektrisch veld
|
|
Als een condensator
opgeladen is, heerst er tussen de platen een elektrisch
veld:
|
U
E = ____
e
|
|
|
E in Volt/meter
U in Volt
e = afstand tussen de platen in meter
|
|
|
|
Technologische
aspecten :
|
|
Er bestaat een ruime
keuze aan condensatoren, alle met specifieke
eigenschappen. Sommige zijn stabiel in het domein van HF,
andere werden voor grote stromen ontwikkeld, weer andere
voor bijzondere toepassingen kunnen gepolariseerd zijn (
let op het '+' en '- ' merkteken op de condensator
).
In het domein van de
zeer hoge frequenties kan onder andere de bedrading van
een condensator een hinderlijke inductie of een verhoging
van de capaciteit betekenen. In zo'n geval moet men
speciale condensatoren gebruiken.
Condensatoren voor hoge
spanningen moeten hierop voorzien zijn bij de keuze van
hun diëlectricum. Er zijn dus heel wat aspecten waar
men op moet letten.
Het is dus duidelijk
dat men het juiste type condensator op de juiste plaats
moet gebruiken.
|
|
|
|
|
|
|
|
De
aanduidingen :
|
|
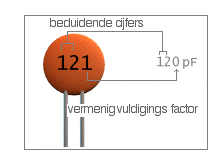
Net zoals bij
weerstanden is het mogelijk de waarde en andere
informatie op de condensator af te lezen. Rechts zie je
een voorbeeld van een markering.
Let op: het laatste
cijfer is de vermenigvuldigingsfactor. Hier toegepast: we
lezen 12 als cijfers en 10 exponent 1 of gewoon 10 als
waarde waarmee men de andere cijfers moet
vermenigvuldigen. Dus 12 x 10 of 120 pF.
Het type condensator
wijst uit welke eenheidsmaat gebruikt wordt.
|
|
|
|
|
Bij
uitvoering van herstellingen :
|
|
Condensatoren zijn de
onderdelen bij uitstek die het in een elektronische
schakeling begeven. Defecte toestellen vertonen zeer
dikwijls één of andere defecte condensator
of ÈÈn die zodanig in waarde is verlopen
dat de kring niet meer werkt zoals bedoeld. De oorzaak
kan zijn :
1 - het lek door het
diëlectricum (vooral bij elektrolytische
condensatoren )
2 - kortsluiting
doorheen het elektrolyt.
In het eerste geval zal
door de lek de waarde zodanig kunnen veranderen dat de
werkelijke waarde nog weinig met de beoogde waarde te
maken heeft. De kring gedraagt zich dan niet meer volgens
het concept. In het tweede geval zal door de tijd de
condensator steeds meer gaan opwarmen en mogelijk zelfs
ontploffen. Hij zal eerst wel opwarmen, wat al een
aanwijzing kan zijn.
|
|
|
|
|
|
|
|
Cyclisch laden
en ontladen
Hier komen we later nog wel op terug, maar toch nog
dit:
|
|
|
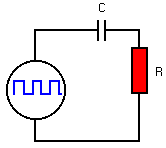
Zie het schema rechts. De blauwe kanteel is een generator
voor een vierkantvormig signaal, aangelegd aan een
condensator in serie met een weerstand.
Een oscilloscoop is een
toestel waarmee men de vorm van elektrische signalen kan
zien. We gaan de golfvorm op de condensator als
gevolg van de vierkantgolf onderzoeken.
|
|
|
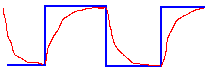
Het
resultaat.
|
|
|
- In het blauw de
spanning zoals deze uit de generator komt.
- In het rood de spanning op de klemmen van de
condensator.
|
|
We stellen een verschil
in vorm vast. De weerstand beperkt enigszins het laden
van de condensator. Omdat de laadstroom kleiner is, zal
er meer tijd nodig zijn om het maximum te bereiken. Als
de weerstand zeer groot is kan het zijn dat het maximum
niet wordt bereikt ( de rode lijn komt niet tot het
horizontale blauwe deel ). Keert de polariteit om, dan
gaat de condensator zich op een gelijkaardige manier
doorheen de generator ontladen. De eigen (of inwendige)
weerstand van de generator tellen op we bij die in de
schakeling .
|
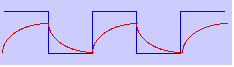
Hier hebben we een
grotere weerstand verkozen. Het maximum van de spanning
wordt niet gehaald.
|
|
Wiskundige wet voor het laden en ontladen
|
e
- t/RC
|
|
|
De logaritme in basis
van het getal e (2.72)
|
|
RC noemt men de
tijdconstante:
één
tijdconstante is de tijd, nodig om 63 % van de maximum
spanning te bekomen.
Men zegt dat een condensator
na 5 tijdconstanten "RC" volledig geladen
is.
|
|
De spanning over de
condensator kan bij opladen na een tijd "t"
volgens deze formule berekend worden:
|
V = E
(
1
- e
-
t/RC)
|
|
Omgekeerd zal deze
spanning bij ontladen volgens deze formule
berekend worden:
|
V = E (
e
-
t/RC)
|
|
|